量子力学的困境与出路
——读温伯格的《量子力学的困境》一文有感
司 今(jiewaimuyu@126.com)
量子力学的困境与出路——读温伯格的《量子力学的困境》一文有感 https://www.toutiao.com/i6432261576203436545/?tt_from=weixin&utm_campaign=client_share&wxshare_count=1×tamp=1537855732&app=news_article&utm_source=weixin&iid=32548838421&utm_medium=toutiao_android&group_id=6432445965295616257
弱电统一理论提出者,诺贝尔物理学奖获得者—Steven.Weiberg
最近,在网上有幸拜读了温伯格的《量子力学的困境》一文,感触良多,现记录下来,与大家分享,但愿喜欢拍砖的“官科”学者和“高等学府”的学子们在此给予“尝试”机会和宽容!
温伯格作为一位诺贝尔物理学奖获得者,他有资格谈“量子力学的困惑”,这么多年来,他一致活跃、挣扎在对当前物理学的反思之路上,为热爱物理学的“科学爱好者”提供了一片新的思考天地和动力,我由衷佩服他为真理孜孜不倦,不愿躺在功劳簿上享受的精神。
概观温伯格的文章,可以看出他是一位量子力学“还原论”的积极倡导者和思考者,他对量子力学的困惑思路和心境与爱因斯坦相仿——生命与一切宇宙奇迹都是遵循物理学规律而动的基本粒子的舞步,即这个世界都可以还原为粒子的物质(或场)及其相互作用。
在国外,有不少大有建树的物理学者走在物理学反思的路上,但反观我们国家,在这条路上走的人却寥寥无几,在当下中国积极倡导“科学创新”的氛围下,这种沉默氛围不得不令人深思。
创新就是要与原来“不同”,但我国的“物理学家”们为什么这么“沉静”呢?——这是一个沉重的话题,其中有国内学术环境因素的影响和压抑,更有懒惰、享受的物质因素束缚和诱惑……
我在转载此文时,觉得「知社学术圈」编辑题的「按」很好:
“20世纪头十年间量子力学的发展给许多物理学家带来冲击。时至今日,尽管量子力学已经取得巨大成功,关于它的意义与未来的争论却仍在继续。
温伯格因统一弱相互作用与电磁作用而荣获诺贝尔物理学奖,其对量子力学本质的思考和挣扎,尤其发人深省”。
——随着新实验与新科技的快速发展,对量子力学理论,我们确实需要“继续讨论”和深刻反思了!
物理学本是探索物质运动规律的科学,但量子力学“几率波”、“测不准原理”等却抹杀了物理学探索中所应秉持的这一基本初衷,至于“真空不真”、“无中生有”等更显得荒诞不经——纵观《量子力学的困境》一文,温大师深深感到现代物理学的危机与迷茫,这正是我与此文产生共鸣的根本所在,现择录该文的几段内容供大家分享和思考:
1、电子波并非是电子物质的波,这和海浪是水波完全不同。电子波是概率波……概率通常被看作是那些还在研究中的不完美知识的反映,而不是反映了潜在物理学定律中的非决定性。
2、我也不像以前那样确信量子力学的未来。一个不好的信号是即使那些最适应量子力学的物理学家们也无法就它的意义达成共识。这种分歧主要产生于量子力学中测量的本质……如果我们忽略其他关于电子的一切而只考虑自旋,那它的波函数跟波动性其实没什么关系。
3、把概率引入物理学原理曾困扰物理学家,但是量子力学的真正困难不在于概率。困难在于量子力学波函数随时演化的方程,薛定谔方程,本身并不涉及概率……如果我们认定整个测量过程都是由量子力学方程来确定,而这些方程又是确定性的,那量子力学中的概率究竟是怎么来的呢?
4、对我来说似乎它的问题不仅仅在于放弃了自古以来科学的目标:寻求世界的终极奥义。它更是以一种令人遗憾的方式投降……有些物理学家采用工具主义的方法,他们声称我们从波函数中得到的概率是客观存在的概率,不依赖于人们究竟有没有做测量。我则不认为这观点是站得住脚的。
5、在现实主义者的观点中,这个世界的历史时时都在进行无穷无尽的分裂; 每当有宏观物体伴随量子状态的选择时历史就会分裂。这种不可思议的历史分裂为科幻小说提供了素材[12],而且为多重宇宙提供了依据,众多宇宙之中某个特定宇宙历史中的我们发现自己被限定在条件优渥从而允许有意识生命存在的历史中的一个。但是展望这些平行历史令人深深不安,同其他很多物理学家一样,我倾向于单一存在的历史。
尽管一些现实主义的尝试已经得到类似于波恩定则这样和实验配合很好的推论,但我觉得他们都不会取得最终的成功。
6、纠缠带给爱因斯坦对量子力学的不信任感甚至超过概率的出现。针对量子力学的缺点又应该做些什么呢? 其实如何去用量子力学并无争议,有争议的是如何阐述它的意义。
如何在当前量子力学框架下理解测量的问题或许是在警告我们理论仍需要修正。量子力学对原子解释的如此完美,以至于任何应用到如此小的对象上的新理论都和量子力学近乎不可分辨。但是或许新理论可以仔细设计,使得大物体比如物理学家和他们的仪器即使在孤立的情况下也可以发生快速的自发式坍缩,从而由概率演化能给出量子力学的期待值。发明新理论的目标即是如此,但不是通过给测量在物理学规律中一个特殊地位而达成,而是使之作为那些成为正常物理进程的后量子力学理论的一部分。
发展这样新理论有一个困难是实验没能给我们指明方向—目前所有的实验数据都符合通常的量子力学。我们倒是从一些普适原理中得到些许帮助,但是这些都最终令人惊讶的演变为对新理论的严苛限制。
7、可惜的是,这些对量子力学修正的想法不仅带有推测性质而且还很模糊,我们也不知道应该期待量子力学的修正究竟有多大。想到此处更是思及量子力学的未来,我唯有引用维奥拉在《第十二夜》中的话:
“O time, thou must untangle this, not I”[1]
……,……,……

思考着的温伯格
读着这些内容,我仿佛感受到温伯格大师对量子力学现实的困惑与发展前景的忧虑;他是一位有责任、敢担当和好进取的、真正融入理论物理学探索天堂的高傲灵魂!
我仿佛又觉得,温伯格思绪里充满了对量子力学清晰“图景”的渴望与“给量子力学找到回家的路”的畅想与憧憬……
在哲学意义上讲,温伯格是“还原论”支持者,他曾主张:还原论的世界是冷漠的,没有一点人情味的。但我们必须忠实地接受他,不是我们喜欢,而是因为世界本来就是这样运行的。
下面就量子力学让人“困惑”的几个问题作以简介并给出我的一点不成熟看法,以期抛砖引玉、深入交流:

1、光与电磁波问题
1.1、光是电磁波的确立基础问题
麦克斯韦将光归咎为电磁波的唯一基础是√ke/km=3×10^8m/s,这种推理是以F=qvB=qmH为假设条件的,但这个等式的物理本质是隐藏了“惯性质量为什么与引力质量相等”的问题,这个问题本质上是“地地道道”的粒子问题,与波没有半点关系……

麦克斯韦与电磁波
我们知道,麦克斯韦在确定km时存在二个隐形假设,即:
(1)、Fe=Fm,这说明他对“光也是一种电磁波”的推断是建立在库伦电荷力与磁荷力是同一种力基础之上的,即他首先将电、磁力作了“统一”假定。
(2)、H=B,由此得出qm=qv,这说明磁极是电荷运动产生的,即静止电荷并不产生磁极;静态电荷之间的力来自于电场,运动电荷之间的力来自于磁场。
不过,依据这二种假设,我们也可以给出另一种推断:
假如F= keqQ/r2= kmqm1qm2/r2成立,则可以得出:ke/km=qm1qm2/qQ;
假如qm=qv成立,代入ke/km= qm1qm2/q Q中,则可得出: ke/km= v1•v2;
这说明,对于导线中运动的电荷而言,二根导线产生力作用是由于运动电荷通过导线时转化成了磁极,但电荷电场并不参与二根导线间力的形成;可见,二根导线之间之所以产生力是由于电荷有运动速度v1、v2的存在,这是二根通电导线力产生的要素,这可没有反映力传递速度问题,更没有说力传递需要光参与,而且力传递与光速也不存在必然联系。
由此可见,麦克斯韦所推出的c值,并不是真正物理意义上的光速,它只不过与光速数值有巧合罢了;如果以此认为麦克斯韦证明了“光也是一种电磁波”,那也只能算是他对光认识的一种“曲解”之举;光与麦克斯韦电磁波概念应存在本质区别!
具有论述请参阅《麦克斯韦得出“光是电磁波”的结论合理吗?》、《关于光与麦克斯韦电磁波本质区别问题的探讨》二文。
1.2、赫兹实验问题
在电磁学发展史中,关于赫兹实验是否能够证明麦克斯韦的电磁波理论是有争议的,比如,时任英国皇家协会会长G.斯托克斯就认为“赫兹实验”只是一种普通的电磁感应现象,并不能证明麦克斯韦电磁波理论;即使我们现在“承认”赫兹实验证明了麦克斯韦电磁波的存在,但它也不可能证明光也是电磁波。

赫兹实验
如果光真的是电磁波,那么,光可以被物体遮拦,电磁波却可以穿过;光被物体接收时会产生热效应,电磁波就没有;光可以成像,电磁波就没有;一束光可以被“提出”单光子,一列电磁波就不可能……
既然光和无线电波是同类东西,为什么还会有如此大的差异产生呢?
LC 振荡能够产生二种效应:(1)、电磁感应效应,这就是麦克斯韦所说的电磁波,(2)、激发辐射光子效应,它就不再是电磁感应现象,而是一种热效应现象。

因此说,赫兹实验只能证明LC振荡会发出一种可以被另一个金属体接收的能量,这种能量是粒子、是感应磁场、还是电磁波?他并不能给出本质上的确定和证明。

2、黑体辐射问题
黑体辐射是指由理想放射物放射出来的辐射,在特定温度及特定波长下会放射最大量的辐射,而黑体是可以吸收所有入射辐射的物体,不会反射任何辐射。
理想黑体可以吸收所有照射到它表面的电磁辐射,并将这些辐射转化为热辐射,其光谱特征仅与该黑体温度有关,与黑体的材质无关;从经典物理学出发推导出的维恩定律在低频区域与实验数据不相符,而在高频区域,从经典物理学的能量均分定理推导出的瑞利-金斯定律又与实验数据不相符,在辐射频率趋向无穷大时,能量也会变得无穷大,这一结果就被称为“紫外灾变”。

黑体模型
1900年,马克斯·普朗克将维恩定律加以改良,又将玻尔兹曼熵公式重新诠释,得出了一个与实验数据完全吻合普朗克公式来描述黑体辐射;但他在诠释这个公式时,通过将物体中原子看作是微小量子谐振子,为此他不得不假设这些量子谐振子的总能量不是连续的,即总能量只能是离散的数值(这与经典物理学观点相悖),即单个量子谐振子吸收和放射的辐射能是量子化的,即ε=hγ.

偶极子振荡模型
物理学对黑体辐射现象解释的物理模型是谐振动模型,而谐振子模型是洛伦兹为了解释LC振荡会产生电磁波辐射而建立起的偶极振子模型,这是一个唯像模型,它是由简谐振动模型抽象而来的;因此,普朗克黑体辐射公式“假设”出的能量子ε=hγ“天生”就带有波性(频率姓)就不足为怪了,这种假设也为今后研究粒子运动埋下了“波粒二象性”的种子;但这里值得我们反思的是,一个物体辐射能量真的就是像谐振子模型所描述的那样吗?黑体长时间辐射有没有质量损失?如果有,那么黑体辐射是一种“跃迁”或“裂变”,还是一种“偶极子”振荡?
追问这些问题,让我们看到了黑体辐射解释的多样性,偶极振子模型仅是其中一种,且是唯像的,除将辐射能量定义为与频率有关的能量子之外,还应存在其他描述方式。
3、波粒二象性问题

波动论下的棱角散射
托马斯▪扬用波动论解释了光“衍射”现象,但仔细分析这种研究观点和方法,似乎存在“偏颇”,据现代实验证明,光的窄缝衍射现象不仅与窄缝宽度有关(要求λ≈a),而且还与窄缝组成材料、窄缝厚度等都有关联,这是波动论无法解释的;而当我们站在粒子有自旋磁矩、窄缝空间有磁场性的观点上看,粒子衍射的本质就是带有自旋磁矩的粒子通过磁场空间时会产生像自旋磁陀螺那样的曲线运动的结果,这种结果不但与自旋粒子磁性大小有关,还与窄缝间距、组成材料、厚度等有关。

粒子论下的棱角散射

牛顿色散实验与电子衍射
如图-1所示,任何粒子自旋都自旋磁矩存在,当它们通过物质磁场空间时,就会产生切割磁力线运动和磁场梯度力运动,这二种运动的合运动就会使光通过磁场空间后产生“转弯”,即所谓的衍射现象;这一现象之所以能够迷惑物理数百年,其主要原因就在于我们考虑光运动时,并没有将光子看作是具有自旋与自旋磁矩存在的粒子、以及物质组成空间在纳米尺度下会呈现明显磁场效应的结果。

图-1 电子自旋磁矩及量子空间与经典空间差异
如果我们仍不将粒子自旋磁场性与物质组成空间内的磁场性相结合,想找出粒子运动产生波粒二象性的根本物理机制,那将是一件不可能的事;光的理论也将永远只能停留在波粒二象性的认知上裹足不前!
4、薛定谔方程物理意义问题
在物理学发展史中,没有哪一个公式会像薛定谔方程那样,给人带来的困惑和争论旷世不衰,人们争论的焦点就在于:薛定谔方程本是描述粒子运动有确定轨迹的经典波动方程,为什么它会“符合”几率波分布呢?

薛定谔与他的波动方程
在这场争论中,前有薛定谔本人、爱因斯坦、普朗克、洛伦兹等,后有费曼、温伯格等;但迄今为止,仍然没有任何一位理论物理学家敢于声称自己读懂了薛定谔方程,因为这套方程纯粹是根据实验数据而总结出来的“经验性公式”,它的“提出”即没有任何物理原理作支撑,也没有描述任何“确定”的物理几何图景,其正确性只能靠“测量”来检验;因此,就连喜欢用数学思维解决物理问题的海森堡都对薛定谔方程感到不满意;他在写给泡利的信中谈道:我越是思考薛定谔理论的物理意义,就越是感到恶心。薛定谔对他那套理论的形象化描述简直毫无意义。换一种说法,纯粹就是些扯淡的东西!但我们今天学习和运用的还是这个几率波方程,为什么呢?因为直到现在人们还没有参悟到薛定谔方程所描述的粒子运动的真正物理机制,也没有出现更好的诠解理论。
从目前物理学给出的薛定谔方程的推导过程中可以看出,这个方程之所以能够“化腐朽为神奇”,关键在于他引入了普朗克能量子E=hγ和德布罗意物质波方程P=mv=h/λ,将机械波方程中的T、λ转换成用动能E和动量P来描述,即

原来量子力学将薛定谔方程改造成波函数后,它描述的本质不再是一个粒子连续时间段的运动方程,而是一个粒子不同时刻或一群粒子在同一时刻运动所应遵循的函数,对其运动结果测量做统计,就会得出它们具有“几率性”;由此可见,几率性不再是对一个粒子连续运动的求解,也就无法得知粒子运动为什么要遵循薛定谔方程了。
薛定谔方程描述一般采用球或柱坐标,在这种坐标系中,一个立体螺旋的投影是正弦或余弦波,那么一个质点在柱坐标或球坐标系中作螺旋运动时,其运动轨迹方程中的x或y值的描述形式就与机械波方程相同。
我们以柱螺旋运动为例:如图-2-1所示,一个作柱螺旋运动的质点,其运动轨迹是一个柱螺旋,它的侧投影就是如图-2-2所示的质点正弦或余弦波曲线,质点在柱坐标系下的运动方程可以描述为

.这与质点柱螺旋方程组中的y值描述形式是一致的,这不得不说,从立体空间上看机械波方程应可以视为柱螺旋方程的一个侧投影形式。
我们从电磁学教程中知道,带电粒子在均匀磁场中可以产生柱螺旋运动,如图-3所示,当电子被射入的速度v与均匀磁场B不垂直时,则电子就会在该磁场中作这种柱螺旋运动。

图-3 电子在均匀磁场中的柱螺旋运动
这说明一个带电粒子要做稳定柱螺旋运动,其运动空间就必须有均匀磁场存在;而薛定谔方程描述的自由粒子运动(即不受任何场影响的粒子运动)如果有波动性,那么让粒子产生y方向运动的物理因素是什么?粒子的波动性应该来自于自身场与空间场的相互影响,而它不可能会无缘无故的“上蹿下跳”地往前跑。
同时,薛定谔方程本身并没有包含粒子自旋与自旋磁矩要素,这说明他还是将粒子看做是经典粒子;狄拉克虽然点出了自旋问题,但却没有做更深入论述。
可见,要想破解薛定谔方程的真正物理意义,就必须将能量守恒、粒子自旋及自旋磁矩性、物质空间的场属性等完全结合起来才行,具体论述请参阅司今《重新解读薛定谔方程——对薛定谔方程物理意义及其所描述的粒子运动物理机制的探讨》一文。
5、几率波问题
量子力学所说的“几率波”不同于水波或电磁波,而是一个统计学概念,故它不是真正意义上的波形式。
“几率”通常被看作是那些还在研究中的不完美知识的反映,而不是反映了潜在物理学定律中的非决定性,是一个宏观次(个)的统计概念,这对于单个事件则是不适用的,如温度就是一个统计意义上的概念,只有几个分子的系统,定义温度概念是没有太大意义的,只有当我们需要在统计意义上研究系统时,温度概念才有必要性。
对一个硬币,当我们将它抛向空中时,它落地后是处于“正面”还是“反面”向上呢?我们不得而知,但我们抛投很多次后发现,它“正面”向上的次数与“反面”向上的次数几乎相等,这就是对宏观(次)统计的结果,这个结果对研究单次抛硬币确定其是“正面”向上还是“反面”向上没有任何帮助。
要想值得每次抛投的确定结果就必须从抛硬币的力学角度进行分析,如,硬币的半径、厚度、质心、被抛时受力点、倾斜面角度、转动摆动情况、受空气阻力情况等诸多力学要素进行综合分析,这样就完全可以确定所抛硬币下落后的正反面确定状态了。

抛硬币与正反面几率
可见,量子力学在描述粒子衍射或绕有心力场运动时,并没有从粒子所受的力因素方面进行考虑,而是采用了宏观统计方法进行描述,这种描述对确定单个粒子运动行为没有任何帮助。
其实,几率波的出现是我们对粒子束认识不足造成的;粒子束中粒子运动是有序的还是杂乱无章的?我们选择了杂乱无章,这就为结果的“几率性”认识埋下了“伏笔”。
张天蓉老师在《拿什么拯救你量子力学》一文中说:“温伯格的疑问表面看起来是从数学角度发出的问题:方程不涉及概率,为何最后的结果中就解释成了概率?事实上,从物理的角度看也是如此,概率的入侵搅浑了量子力学,搅浑了物理学家们的科学思维方式”[2];
我赞同张天蓉老师的看法,几率波的引入无疑是对微观物理学的嘲弄与讽刺!
6、测量与波函数崩塌问题
波函数坍缩是用波函数去描述微观领域粒子运动现象下而“制造”出来的物理“怪现象”;我们知道微观领域的物质具有波粒二象性,表现在空间分布和动量都是以一定概率存在的,比如“电子云”,将之称为波函数。当我们用物理方式对其进行测量时(同时必然对其干扰),物质随机选择一个单一结果表现出来。如果我们把波函数比作是骰子的话(比如电子云),那么“波函数坍缩”就是骰子落地(比如打在屏幕上显示为一个点的电子)。

显像管原理图
物理学家李淼曾这样解释波函数崩塌问题:
“上个世纪二十年代,海森堡发现,所有客体,主要是微观粒子如电子,如果你不去观测它,它的状态是不确定的。比如,当我们用确定电子位置的仪器去看电子之前,电子的位置是不确定的,根本不知道它在哪里。一旦我们去看它,它瞬间就出现在某个位置,海森堡说,这是因为电子本来不确定位置的“波函数”因为人的观测瞬间塌缩成某个确定位置的“波函数”了。

电子波函数“崩塌”与显像
后来,进过很长时间的发展,物理学家找到波函数塌缩真正的原因:电子和仪器,即一个宏观体系相互作用时,和这个体系发生了纠缠。比如,如果我拿一个荧光屏去拦截这个电子,这个电子必然和荧光屏里的大量感光分子中的一个发生了反应,让这个分子发光,它的位置也同时确定了”[3]。
我赞同他的解释观点,因为任何测量仪器都是由带有自旋磁矩的分子、原子、电子等组成,在这个组成体“近距离”空间(如纳米空间)下就必然会表现出较强的磁场性;当我们拿这个仪器在一定“近距离”空间去测定一个带有自旋磁矩的粒子运动动能时,这个粒子的运动速度就会受仪器“近距离”磁场影响而产生变化;如果我们没有看到测量仪器磁场影响因素的存在,就必然会得出“测不准”结论。
更形象地说,如图-4所示,我们在测量仪上放一块磁铁,用它去测量一个运动铁球的动量与空间位置的关系,这必然会与没有放磁铁的测量结果产生差异;如果我们不考虑磁铁影响因素,就会说这个铁球运动符合“测不准原理”,那么,我们将永远不可能明白铁球运动产生“测不准”的根原,也更不可能发现铁球在仪器磁场中运动变化的物理规律。

图-4 磁体与无磁体空间的铁球运动变化
在无测量状态下,粒子运动被“人为”地认为会遵循薛定谔波函数方程,并以几率态存在,一旦测量,粒子就不会呈几率态,而是呈确定态,这就是量子力学所说的一种波函数崩塌现象。
量子力学所说的测量是指“投影”,而不是“轨迹”,而薛定谔方程描述的是粒子波动“轨迹”;可见,将“投影”用薛定谔方程来解释得出“几率”性来就不足为怪了。其实,“投影”图案的“波”分布性是与自旋磁粒子通过磁场空间时磁场空间有磁场梯度分布,这种分布与粒子束中粒子以“晶格”形式保持“有序”运动分不开的。
可见,量子力学波函数崩塌及测不准问题都是一种唯现象论,它不可能从物理机制上解决粒子出现测不准的原因,也不可能看清波函数及其崩塌的物理本质。要想找出产生此现象的物理原因,就必须将测量仪器的磁场性与运动粒子的自旋磁矩性相结合,这才是出路之本。
7、量子纠缠问题
量子纠缠是量子力学理论最著名的预测,它描述的是由两个或两个以上粒子组成的系统中它们产生相互影响的现象,当然,这个系统空间距离可近可远,但它们的相互影响却不会“消失”,即当其中一个量子被操作(如测量)而状态发生变化时,则另一颗也会即刻发生相应的状态变化,如自旋轴方向始终保持相反。
玻尔曾将量子纠缠称为”鬼魅似的远距作用”,但这并不仅仅是个诡异的预测,而是已经在实验中获得证实的现象。
量子纠缠说明在两个或两个以上的稳定粒子间会有强的量子关联性,那么,这种“关联性”形成的物理基础是什么呢?量子力学回答不了,于是人们“困惑”了……

量子纠缠示意图
对此,我的思考是,单从字面解读“量子纠缠”,既然“纠缠”就应该有力参与,也就是说,量子纠缠的本质应该是一种力现象;
但由于量子力学对粒子的描述思路不同于牛顿力学,即它抛弃了牛顿力概念,取而代之的是用波、动量、动能、自旋等概念去描述粒子运动情况,这种描述由于过于抽象性,必然会将量子现象中的一些现象神秘化,而且如果抽象脱离了实际,其结果必然会得出“无中生有”的结论。
其实,量子纠缠并不神秘,它们的本质就是粒子们自旋所具有的自旋磁场之间相互影响的结果;如果我们站在粒子自旋磁场角度去解读这一现象,则很容易被人们所理解和接受,但如果我们还用经典粒子(没有自旋和磁场性)眼光去审视量子纠缠,则必然会觉得有“鬼魅似的远距作用”之感;在此,我猜玻尔对量子纠缠的困惑就在于他还没有摆脱“经典粒子”思维束缚所致吧。
如图-5所示,当我们把二个自旋磁电子放置在一个相距很远但磁场可以忽略不计的空间,我们用磁探针改变其中一个电子的自旋轴方向,则另一个电子的自旋轴方向就会随之产生相应改变,这才是量子纠缠的物理本质,其中空间磁场要求是趋于0状态。

图-5 电子自旋与纠缠态
8、电子轨道磁矩与自旋问题
8.1、电子轨道磁矩
我们知道,现代物理学关于原子构成模型是基于卢瑟福的“太阳行星模型”展开的,而太阳行星模型运算有二套定量法则:
(1)、开普勒三定律,其中角动量守恒最重要;
(2)、牛顿万有引力定律。

如果将电子电荷也看做是像电子质量一样有实质意义的话,那么,这个轨道磁矩的本质就可以用电子电荷所表示的荷角动量之半来解读;电子绕核运动就像地球绕太阳运动一样,是一个闭合的曲线运动(如不闭合,则它的稳定性就不会存在),它的荷角动量之半就是我们定义的轨道磁矩量。
7.2、电子1/2自旋
电子1/2自旋是人们根据量子力学轨道磁矩定义延伸出来的概念,它是没有经过科学验证、观察到的假设推断,谁也没有从实验中看到电子真的需要自旋720°才会恢复原来模样;而且,就目前实验条件来看,能够真正观察到电子自旋720°才完成自旋一周运动几乎是不可能的,因此,电子1/2自旋观点只能算是一种纯假说,这种假说的真实性应值得怀疑,希望广大物理学研究者能够关注这个假说的合理性与否并予以可靠地验证。
量子力学在解释施特恩-格拉赫实验现象时引入了乌伦贝克和孤兹米特提出的电子自旋假说,教科书的论述是这样的:

施特恩-格拉赫实验示意图


从上面的解释中可以看出,因银原子束通过施特恩-格拉赫磁场空间时产生了上下二条曲线分布,依据玻尔的电子绕核运动理论,则电子在核外的轨道分布数是按2L+1形式分布的,如果将银原子看做是绕施特恩-格拉赫磁场作轨道运动,则它也一个遵循2L+1轨道数分布,但银原子通过磁场空间后产生的是二条曲线,故由2L+1=2推理出L=1/2;但量子力学规定,绕核运动的电子总轨道角量子数和总轨道磁量子数都应是整数,这就违反了量子力学原理,于是他们就引入了电子自旋。但因L=1/2,于是就假定电子自旋的量子数(自旋角动量)是半整数,由此提出电子自旋为1/2形式。实验还证明,电子有磁性,于是就将电子1/2自旋与其自旋磁矩性诠解为电子的内禀性;同时,如果按目前给出的电子经典半径(2.8×10-15m)计算,电子要想达到h数量级的角动量,其表面线速度就会大于光速百倍,这就违反了光速不变原理,于是,为了“自圆其说”, 量子力学就不得不把电子自旋说成是不同于经典概念的自旋。
但现代物理学证明,电子真实半径目前还没有能力测出确切值,丁肇中教授在《寻找宇宙中最基本的粒子》讲座中提到,在10×-17m以下也无法测出电子半径,其他物理学家预言电子半径应在10×-20m以下,如果以电子半径r=10×-17m计算,电子自旋面速度也不会超光速呀;如此看来,用电子面速度超光速来否定电子自旋经典的经典刚体性的理由是不充分的;再说,电子1/2自旋是用量子力学法则“假设”出来的,并不代表自然界就真实存在1/2自旋粒子。
就目前较成功的核磁共振理论及电子巨磁阻理论等来看,它们还都是将电子看做是一个实实在在的小自旋磁陀螺来对待的。

电子可以看做是小自旋磁陀螺
从电子1/2假说到到超光速验算可以看出,量子力学将电子自旋说得如此神乎其神是与科学精神相悖的,因为我们不应将施特-恩实验中原子分裂成二条曲线的物理行为与电子绕核运动的轨道分布行为相提并论,它们是二种不同引力场中的不同运动形式。按我的“自旋场理论”分析,银原子在“上下型磁场”中运动时会产生二条曲线分布形式,而自旋磁电子绕磁原子核运动是在“中心型磁场”中运动时才会表现出量子化轨道分布形式。
当然,在施特恩-格拉赫实验磁场中,用氧等偶核原子作实验时会产生2L+1条曲线分布,这是因为偶核原子表现的磁矩太小而产生像光衍射条纹一样的行为所致,即在缝中心处由于偶核磁矩弱,上下型磁场磁极不能对它们产生明显磁影响,结果它们就只能以近乎以直线运动形式穿过窄缝磁场空间,并在到达后接受屏时呈近乎直线分布;但对于靠近磁场磁极的偶核原子就可以感受到明显的磁极影响,于是它们就会在后接受屏产生向上或向下的曲线分布,而且这种曲线分布条数遵循2L+1规律。
由此,我们说,将电子定义为1/2只是为了迎合量子力学法则而人为规定的行为,这并不代表自然界中真的存在1/2自旋形式的电子;而且,电子的真实半径到现在还是个谜,量子力学用“电子自旋超光速”来否定电子自旋的经典刚体性的理由就不充分。

电子1/2自旋示意图
在电磁学中,电子之所以被看做是点粒子,是因为对它的讨论不牵扯到磁矩问题,但在量子力学中,如果再将电子看做是点粒子,这就与电子的自旋磁矩概念存在冲突,因为磁矩描述的是与空间r有关的量,即电子半径不可能是0,否则自旋磁矩存在就无从谈起。
鉴此,我认为自旋磁矩概念不适合描述点电子的自旋磁性行为,我们应该抛弃自旋磁矩概念,引入点粒子偶磁荷概念,用自旋“角动量”qm=mω来取代自旋磁矩概念将比较符合实际,而且也不会再出现“1/2自旋”、“ 内禀性”等不可理喻的描述形式,对此论述可参阅司今《从角动量守恒看qm=Mω 的物理意义》一文。
9、量子力学研究对象及范围问题
量子力学研究的对象是有自旋和自旋磁矩的粒子在磁场中运动,如格拉赫实验、塞满效应(反常塞曼效应)、核磁共振、粒子衍射等,无不是在磁场条件下产生的;但我们探讨粒子衍射现象时,却从不去专注粒子自旋磁矩性和空间磁场性,只一味地就现象而现象的去研究量子衍射问题,这是一种“舍本求末”的做法。
粒子运动表现出所谓“波”性的根源是自旋磁粒子与空间磁场相互作用时所产生的一种“转弯”运动现象,从力学角度讲,它们产生这个现象的原因有二个方面:
(1)、自旋磁粒子在磁场中作平面“转弯”运动(即磁场洛伦兹运动);
(2)、自旋磁粒子自旋磁轴方向受磁场磁极影响而产生的磁场梯度力运动(即施特恩实验中所描述的F=μdB/dz)。
量子力学研究的对象是微观粒子,而且是带有自旋和自旋磁矩性的粒子,这些运动就类似于自旋磁陀螺的平动与进动一样,都可以在球坐标系中用相同的方程去描述。
而且,量子力学中的量子只是描述微观世界粒子性的一个笼统概念,它应包函可以独立存在的任何形式粒子,如质子、中子、电子,光子等都可以在各自的研究领域内称为“量子”。

电子、质子自旋及其磁矩
当我们研究量子问题时,量子的几个重要物理属性值得大家关注:
(1)、能量不连续性,即普朗克所描述的传递能量的粒子是“一份一份进行的”;
(2)、角动量不连续性,比如电子在核外分别时,其轨道角动量是不连续的,具有量化“跳跃性”;
(3)、运动的自旋性和自旋磁矩性,量子描述的世界是一个带有自旋和自旋磁矩性运动的物质世界,这与经典力学中的粒子概念不同。
“自旋生磁”是我的“自旋场理论”的重要组成部分,当然,磁的产生还包括“公转生磁”,这说明磁的产生应有二种形式,即“自旋生磁”和“公转生磁”;但目前电磁学和量子力学只研究了“公转生磁”,却忽略了“自旋生磁”性,这是当今物理学存在严重“疏漏”的地方,值得去大家关注!

磁场空间下的磁陀螺、电子及地球运动对比图
从量子的上述“属性”来看,我们对量子概念还可以再拓展:在一个研究系统中,凡是具有自旋、自旋磁矩性存在的独立系统或个体都可以归纳为一个“量子系统”,从这个意义上来说,电子的洛伦兹运动也被可以看做是一种量子运动;同样地,太阳系中行星的运动也可以被看做是一个“量子系统”,因为太阳与行星都有自己的自旋磁场,如将地球看做是一个“量子”的话,那么,站在自旋和磁矩角度看,对“地-太”系的研究也可以纳入量子力学范畴……

带有自旋磁场的地球
10、量子力学出路问题
量子力学是研究质点自旋运动的力学,它不能放弃“波粒二象性”认识的根本原因在于我们无法用经典粒子概念来解释光的“衍射、干涉”等具有波性的现象。
在经典粒子概念中,粒子是没有自旋和自旋磁场性,粒子通过的物质空间也没有磁场性。但现代物理学已证明,质子、中子、电子、光子等都具有自旋和自旋磁矩性,这说明它们已不同于经典粒子,它们具有自旋和磁场双重性;但量子力学在探讨光衍射现象时,倒是把光的这一本质性给忘记了,同时也忽略了由自旋粒子(如质子、中子、电子等)组成的窄缝空间也是一个磁场空间;试想,一个有自旋磁矩的粒子通过一个有磁场的空间,这个粒子运动还会像经典粒子那样作直线运动吗?
如果我们认真地将粒子们的双重性与物质空间磁场性有机结合起来,我想,解决粒子“干涉、衍射”问题并不难,关键难得是我们将如何改造与舍弃我们现有的量子力学?如何补充与完善我们的经典物理学?
我们要始终牢记,微观世界的物体运动与宏观世界的物体运动存在本质区别,那就是在我们眼里和经典理论中,宏观物体运动是没有自旋与自旋场集于一身的物体;更要牢记,空间宏观物体的磁场对其他物体运动的影响要比微观世界小得多,对此我们可以从目前纳米材料的属性实验中得到验证。
“波粒二象性”不是研究微观世界的真正出路,把握微观世界粒子的自旋与自旋磁场性及微观空间的磁场性才是我们真正打开微观世界大门的一把金鈅匙。

用磁陀螺运动解释光子衍射现象[5]
我们必须抛弃“波粒二象性”思想,回归到创新的经典力学中来,这是量子力学今后发展必须付出的代价!但就目前来看,我们的物理学主流界能答应吗?
一个理论的正确与否关键在于可不可以通过实验验证,验证就要有一个清晰的模型图景;在宏观世界中,我们能够找到有“场与自旋”的物理模型非“自旋磁陀螺运动”莫属了,因此,我的“自旋场理论”就是从研究“磁陀螺在磁场中运动”开始的。

我认为,将来的量子力学必然是带有自旋磁场的质点运动与空间或物质自旋场有机结合的力学,这种结合是对牛顿质点力学与库伦“点荷”理论的回归;用研究、对待自旋磁陀螺的眼光来重新审视微观世界的那些“精灵们”,像牛顿力学体系那样,从“公理”出发,建立我们微观世界的真正物理理论体系,这样,我们的物理学才能真正走进微观世界的殿堂,才能真正走进量子大时代!
我期待着这一时刻的到来!

风雨过后见彩虹
11、结束语
量子力学带给人们的困惑主要起源于我们对量子及物质空间的理解总还徘徊在“经典”物理学上,比如,对待量子“概率”问题,我们总是忘记量子有自旋磁矩性、物质空间也有磁场性;又如,我们思考量子“纠缠”问题时,总是站在“经典粒子”角度看待这一现象,曾没有从量子有自旋磁场性角度来看待二个量子产生“纠缠”的物理本质;再如,我们在看待波函数崩塌的“测量问题”时,有谁去刻意思考过我们所用的仪器也是带有磁场的物质,它们会造成量子运动状态(自旋和平动)的改变呢?……

纳米空间与粒子运动
量子现象与经典现象的本质区别在于尺度效应,如,处于纳米尺度下的量子世界处处都是由场支配,而经典世界则没有这一要求——场是认识量子世界的灵魂,我们只有守住这一灵魂,才能真正走进量子世界,才能真正摆脱量子力学带给我们的诸多困惑……
【注】
[1] 温伯格《量子力学的困境》:http://chuansong.me/n/1473016951311
[2] 张天蓉《拿什么拯救你量子力学》:http://blog.sciencenet.cn/blog-677221-1054026.html
[3] 李淼在头条:量子坍塌到底是个什现象?
https://wenda.toutiao.com/question/6402115736763891969/
[4] 赵凯华,罗蔚茵/著《量子物理》,高等教育出版社2008年1月第2版,P51~53页。
[5]司今/《从磁陀螺运动谈粒子衍射形成的物理机制》:
http://bbs.sciencenet.cn/thread-3087786-1-1.html
【参考文献】
〔1〕赵凯华/著《光学》,高等教育出版社2004年11月第1版。
〔2〕赵凯华,陈熙谋/著《电磁学》,高等教育出版社2003年4月第1版。
〔3〕【美】Richard P.Olenick,Tom M.Apostol David L.Goodstein/著/李椿,陶如玉 译《力学世界》,北京大学出版社2002年2月第1版。
〔4〕赵凯华,罗蔚茵/著《量子物理》,高等教育出版社2008年1月第2版。
〔5〕费恩曼/物理学讲义(2),上海科学技术出版社,2013年4月第1版。
〔6〕徐龙道等/著《物理学词典》,科学出版社2004年5月第1版。
〔7〕百度图片及「百度百科」相关内容。
大型强子对撞机(LHC)就明确要找希格斯粒子。验证希格斯粒子后,LHC基本任务完成,遗留大量数据继续分析处理。但它已经花了上百亿欧元,很想继续做下去,包括向更高能量发展。
我国在单、双环对撞机分支有些人才,距LHC要求甚远。而在LHC工作的多为数据分析人才。中微子实验离此目标也甚远。
王淦昌先生在1990年代跟我说过,靠加速器要发现TeV级的粒子,几乎不可能。但是TeV级的宇宙射线,虽然不知道原因,总是会来的。我们要发展宇宙射线,花钱不多,耐心积攒数据,到一定程度就有重要发现。






























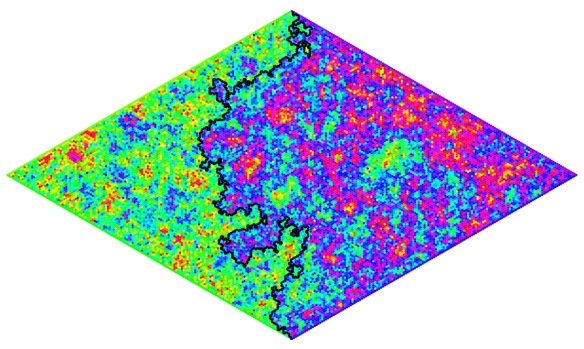




From personal bias, your multiboundary black holes resemble a bronchial tree fractal.
In that same picture where the event horizons are represented by dotted lines, curious what your math shows at the cosmological horizons, the other causally disconnected place in our universe, in the sense that beyond which, like from inside black holes, photons could never reach back to us?
Sean, old pal…
“Before mentioning how I met my collaborators”: did I miss this part or did you leave it out? I’ve heard your Afghanistan story before… and I find you and your life more interesting than your work 😉
Sorry, Shaun, I see I somehow typed the wrong spelling of your name. I encourage you to do the same to me as fitting retribution.
great post, tempted to re-blog it.
GPS, alumni, astronomy, planetary_science, research_news
Massive Astrophysical Objects Governed by Subatomic Equation
Quantum mechanics is the branch of physics governing the sometimes-strange behavior of the tiny particles that make up our universe. Equations describing the quantum world are generally confined to the subatomic realm—the mathematics relevant at very small scales is not relevant at larger scales, and vice versa. However, a surprising new discovery from a Caltech researcher suggests that the Schrödinger Equation—the fundamental equation of quantum mechanics—is remarkably useful in describing the long-term evolution of certain astronomical structures.
The work, done by Konstantin Batygin (MS ’10, PhD ’12), a Caltech assistant professor of planetary science and Van Nuys Page Scholar, is described in a paper appearing in the March 5 issue of Monthly Notices of the Royal Astronomical Society.
Massive astronomical objects are frequently encircled by groups of smaller objects that revolve around them, like the planets around the sun. For example, supermassive black holes are orbited by swarms of stars, which are themselves orbited by enormous amounts of rock, ice, and other space debris. Due to gravitational forces, these huge volumes of material form into flat, round disks. These disks, made up of countless individual particles orbiting en masse, can range from the size of the solar system to many light-years across.
Astrophysical disks of material generally do not retain simple circular shapes throughout their lifetimes. Instead, over millions of years, these disks slowly evolve to exhibit large-scale distortions, bending and warping like ripples on a pond. Exactly how these warps emerge and propagate has long puzzled astronomers, and even computer simulations have not offered a definitive answer, as the process is both complex and prohibitively expensive to model directly.
While teaching a Caltech course on planetary physics, Batygin (the theorist behind the proposed existence of Planet Nine) turned to an approximation scheme called perturbation theory to formulate a simple mathematical representation of disk evolution. This approximation, often used by astronomers, is based upon equations developed by the 18th-century mathematicians Joseph-Louis Lagrange and Pierre-Simon Laplace. Within the framework of these equations, the individual particles and pebbles on each particular orbital trajectory are mathematically smeared together. In this way, a disk can be modeled as a series of concentric wires that slowly exchange orbital angular momentum among one another.
As an analogy, in our own solar system one can imagine breaking each planet into pieces and spreading those pieces around the orbit the planet takes around the sun, such that the sun is encircled by a collection of massive rings that interact gravitationally. The vibrations of these rings mirror the actual planetary orbital evolution that unfolds over millions of years, making the approximation quite accurate.
Using this approximation to model disk evolution, however, had unexpected results.
“When we do this with all the material in a disk, we can get more and more meticulous, representing the disk as an ever-larger number of ever-thinner wires,” Batygin says. “Eventually, you can approximate the number of wires in the disk to be infinite, which allows you to mathematically blur them together into a continuum. When I did this, astonishingly, the Schrödinger Equation emerged in my calculations.”
The Schrödinger Equation is the foundation of quantum mechanics: It describes the non-intuitive behavior of systems at atomic and subatomic scales. One of these non-intuitive behaviors is that subatomic particles actually behave more like waves than like discrete particles—a phenomenon called wave-particle duality. Batygin’s work suggests that large-scale warps in astrophysical disks behave similarly to particles, and the propagation of warps within the disk material can be described by the same mathematics used to describe the behavior of a single quantum particle if it were bouncing back and forth between the inner and outer edges of the disk.
The Schrödinger Equation is well studied, and finding that such a quintessential equation is able to describe the long-term evolution of astrophysical disks should be useful for scientists who model such large-scale phenomena. Additionally, adds Batygin, it is intriguing that two seemingly unrelated branches of physics—those that represent the largest and the smallest of scales in nature—can be governed by similar mathematics.
“This discovery is surprising because the Schrödinger Equation is an unlikely formula to arise when looking at distances on the order of light-years,” says Batygin. “The equations that are relevant to subatomic physics are generally not relevant to massive, astronomical phenomena. Thus, I was fascinated to find a situation in which an equation that is typically used only for very small systems also works in describing very large systems.”
“Fundamentally, the Schrödinger Equation governs the evolution of wave-like disturbances.” says Batygin. “In a sense, the waves that represent the warps and lopsidedness of astrophysical disks are not too different from the waves on a vibrating string, which are themselves not too different from the motion of a quantum particle in a box. In retrospect, it seems like an obvious connection, but it’s exciting to begin to uncover the mathematical backbone behind this reciprocity.”
The paper is titled “Schrödinger Evolution of Self-Gravitating Disks.” Funding was provided by the David and Lucile Packard Foundation.