The Totality in Mathematics and Physics
Li Xiao-Jian1) Gong Jeh-Tween 2) †
- (Department of Automation, North China University of Technology, Beijing 100144, China)
- (Institute of Chinese Etymology, Diamond Bar, CA 91765, USA)
- co author. E-mail: tienzen.gong@gmail.com Tel:(626)369-0926
Abstract: There are many paradoxes in mathematics , as well as in physics, which are caused by the symmetry breaking processes from totality. In revers, the totality can be reached by unification processes. By understanding of the concepts of Symmetry; Symmetry breaking; Complementarity (mutual exclusive); Mutual immanence (mutual inclusive),and Totality, we will reach the final truth.
1.Mathematical way of thinking
A few hundred years ago, Descartes, Euler and many others believed mathematics to be the accurate description of real phenomena and they regarded their work as the uncovering of the mathematical design of the universe. Today, almost all mathematicians believe that mathematics is no longer absolute but arises arbitrarily. So, mathematicians can arbitrarily choose a set of definitions to construct a new mathematics. After the discovery of Godel’s Incompleteness Theorem, even the self-contradiction of a system is no longer a criterion to invalidate a new mathematics.
Strong point: Seemingly, there is no restriction (such as experimental verification, philosophical reflection, etc.) as the domain boundary in mathematics, that is, there is seemingly no unthinkable issue in mathematics. On the contrary, quite a few issues are unprovable in mathematics, such as, Goldbach’s conjecture, etc..
Shortcomings: Mathematical way of thinking still cannot encompass the other ways of thinking,like the physics experiments,and philosophical thinking.
2.The beginning of the beginning
Philosophically, if there is a creator before the Beginning, the Beginning is not the beginning. Thus, the religious reasoning and conviction cannot be understood and supported by philosophy.
Today, quantum cosmology understands the detailed evolution processes of Big Bang from its first one-trillionth of a second to now but is unable to explain what before the Big Bang was.
Many physicists proclaim, “What came before the Big Bang? This is a meaningless question, given that space and time themselves came into being in the Big Bang. Without time, there can be no ‘before,’ just as without space there can be no ‘outside.’
There can be ‘before’ before time, that is, the timelessness which is the complement of time. With the concept of the complementarity, this unthinkable issue will become thinkable.
3.Paradoxes
Russell paradox: proposition A states “All propositions are true,” and proposition B states “Proposition A is false.” Obviously, proposition B must be true if proposition A is true. But, if B is true then A must be false.
Grelling paradox: A word is said to be “autological” if and only if it applies to itself.
Every paradox always contains two truths, but they must be directly opposite of each other both in their meaning and in their internal reasoning processes. Seemingly, every paradox is always unthinkable.
4.How to think about the unthinkable
Seemingly, all paradoxes are always unthinkable. So the solution for thinking about the unthinkable lies in finding out the cause of the paradox. Both the Russell and Grelling paradoxes are caused by a symmetry-breaking process.
The Russell paradox is caused by the attempt to categorize the world with a definition, “what is true?” This categorizing and defining procedure is a symmetry-breaking process. The Russell paradox is created by breaking a symmetry, the totality. When the null term ” T” (the totality) is replaced by “true”, the symmetry of the null proposition (all propositions are “T “) is broken, and the new proposition (all propositions are “true”) creates a paradox with “false”.
Grelling got himself into his predicament by inventing definitions for autological and heterological. Every definition always acts as a symmetry-breaking procedure, separating a totality (symmetry) into categories.
Nonetheless, all paradoxes can be reconciled in two ways, downward or upward solution. The downward solution is obtained by a further downward symmetry-breaking with a new proposition: All propositions “except proposition B” are true. The upward solution is obtained by removing the first symmetry-breaking which causes the problem, and the null symmetry (the totality) is regained.
So, all unthinkable issues will become thinkable when the following concepts are understood.
5.Symmetry
5.1 Symmetry
5.2 Symmetry breaking:
Symmetry always connotes chaos, degrees of freedom. A square peg can go into its mating hole in four ways, a hexagon peg into its mating hole in six ways. The higher the symmetry, the higher the chaos. The highest symmetry has the utmost chaos. For example, a round peg can go into its mating hole in infinite ways.
Symmetry-breaking — complementarity
In physics, most natural symmetries are broken by a special symmetry-breaking process — the spontaneous-symmetry breaking (SSB). For example, a pencil standing upright on its tip can fall in any direction. The probabilities are equal in all directions. So that probability function has a symmetry. But, when the pencil actually falls, the symmetrical probability will be broken into one reality.
The nature phenomena of spontaneous symmetry-breaking were expressed as Copenhagen Interpretation (CI) in quantum physics — the principle of complementarity which consists of three parts.
- A “whole” (totality) must consist of two opposite parts.
- These two opposite parts must be mutually exclusive.
- These two opposite parts are complementary to each other.
In physics, this principle of complementarity is expressed as Heisenberg Uncertainty Principle. In quantum physics, the entire universe is divided into two mutually exclusive but complementary parts. Then, these opposite parts are paired together, position versus momentum, time versus energy, etc., and only one of the two parts can be truly known with a high precision of accuracy by any type of consciousness not only in practice but also in principle according to CI.
6.Totality
Totality is an indivisible symmetry. To break the totality symmetry will create three parts (not two) — totality (itself remains), part one and the symmetry partner of part one. Part one and its partner are always forming a paradox. (Note: to break a symmetry which is not totality will not always create paradox). In physics, it manifests as spooky action or uncertainty principle. In mathematics, it manifests as Godel’s incompleteness theorem.
6.1 Totality in physics (Spooky action and Quantum Entanglement)
Aspect’s experiment leads to the conclusion that the universe cannot be understood by the sum of its parts because the whole (the totality) is utterly indivisible. In fact, all isolated entities can be assumed to have interacted at some point (such as at Big Bang) in the history of the cosmos.
Seemingly, you and I are separated individuals. But, we are linked together in this meeting by our thinking communication. We are linked together by a human society, that is, I am wearing the shoes you made and you are eating the grain I produced.
In fact, our inseparableness is seeded long before our existence. All life forms we know of are carbon-based with water as a chemical solvent. Every heavy atom in our bodies — whether potassium, iron, calcium, carbon, oxygen or nitrogen — had to be produced by the nuclear fusion process (the so-called carbon-oxygen-nitrogen cycle) in the core of stars. Not only is life the reincarnation of those dead celestial bodies, but the calcium in your bones could be the by-product of the iron in my blood.
In short, the totality is absolutely indivisible.
6.2 Totality in mathematics
— Godel’s incompleteness theorem
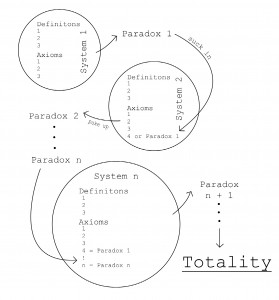
Pic.1 The unification of paradoxes
Today, many physicists believe that physics is complete. Given the laws of physics, the universe can, so to speak, take care of itself, including its own creation. But physics is framed in mathematics, and mathematics is incomplete according to Godel’s incompleteness theorem which warns us that the axiomatic method of making logical deductions from given assumptions cannot in general provide a system which is both provably complete and consistent. There will always be truth that lies beyond, that cannot be reached from a finite collection of axioms.
Since every mathematics system is built upon definitions and axioms, and since all definitions and axioms are symmetry-breaking processes, all mathematical systems must be broken subsystems from a higher symmetry. The incompleteness theorem is, in fact, pointing out the vivid reality of totality in terms of mathematics.
Thus, a mathematics system can suck in a countable number of axioms but can still and must puke up at least one undecidable statement. In short, the first principle (the totality) will always the last dead end, and will burn a hole in every mathematics system invented by men. See the graph on the Pic.1.
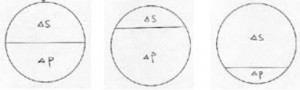
- Mutual Immanence
Although the notion of complementarity accepts the concept of totality in its logical framework, its methodology tries to divide this totality into two mutually exclusive parts. However, the uncertainty principle also means mutual inclusive. See the graph on the Pic.2.
Pic. 2 Mutual immanence
In fact, the indivisible totality which is pointed out by the spooky action can only be understood with a mutually inclusive complementarity, that is, the mutual immanence.
Mutual immanence can best be understood in terms of Chinese philosophy — the Yin and Yang. In time of conflict, yin and Yang are opposite forces. In constancy, they not only complement each other but are imbedded in each other. After reaching their full strength, they transform into the opposite. That is, Yang becomes Yin and Yin becomes Yang.
Mutual immanence is similar to complementarity but with much deeper meanings. Complementarity consists of opposites which are mutually exclusive. Mutual immanence are opposites which are mutually inclusive to make a whole. Consider several pairs of opposites: whole-parts, cause-effect, good-bad, universal -particular. Yet, is there not something about both of the two in each pair that makes them alike?
Today,the quantum computation and communication becomes the most advanced high-tech, which is base on quantum entanglement and the mutual immanence.
8.Conclusion
All paradox issues become thinkable as soon as the following three concepts are understood.
(1)Symmetry
(2)Symmetry-breaking:
(3)Totality
The validity of all unprovable truths (or theories) of mathematics and physics can be obtained by this new method.
References:
[1]. Jeh-Tween Gong, The Divine Constitution,Chicago, Adams Press, ISBN 0-916713 -05-9,1992
[2]http://www.prequark.org/Na1.htm, How to Think About the Unprovable and the Unthinkable
[3]《物理世界与数学世界的统一问题》, http://www.pptv1.com/?p=21
[4]Jeh-Tween Gong, Super Unified Theory , US copyright TX 1–323–231, 1984
[5] Tienzen (Jeh-Tween) Gong,Truth, Faith, and Life , Adams Press, Chicago. 1990, ISBN 0-916713-04-0
[6] Tienzen (Jeh-Tween) Gong,Linguistics Manifesto ISBN 978-3-8383-9722-1,
[7] https://tienzengong.wordpress.com/
[8] http://www.prequark.org/Ftoe.htm
[9]http://www.prequark.org/Gravity.htm
[10] http://www.prequark.org/pq11.htm
[11] http://www.prebabel.info/
[12] http://www.prequark.org/Pq1.htm
[13] 科学方法的正确性问题 , http://www.pptv1.com/?p=324