最近我和朋友们在探讨,量子世界的秘密,宇宙底层的秘密,引力的秘密以及关于量子信息的基础理论。
引力的源头,龚学理论告诉了我们,是时间驱动。
在上一篇博文中,定义了一个最小能量单元:米农(minon)
“我们认为三旋理论还可以往底层发展,甚至还可以远溯到n重三旋底层结构。我们可以采用多重复数,可以运用博特周期性定理描述酉群的同伦群和正交群同伦群的周期性。多重复数的展开形式为标准的U结构。所以,多重复数的同伦周期为 8,在物理意义上同伦的概念可以和性质相似等同。多重复数是现代数学和物理学体系的演绎和发展。通过对多重复数的深入 研究可以进一步揭示客观世界的更深层的规律,从普朗克常数出发,求取该常数下的最小能量值,直达宇宙学常数层面,再迭代回归到普朗克尺度,甚至标准模型粒子尺度、中观物质层面、甚至宏观宇宙。
根据龚学理论确定性方程: (delta E * delta T)=h-bar,能量空间与时间可以具有反对称性。
可取:minon== min delta E ==h-bar/(max delta T),
而max delta T=137–138亿年,是宇宙的年龄。
普朗克常数:h-bar = ħ = 1.0545718 × 10-34 m2 kg / s
C = 299 792 458 m / s = 2.99 x 10 ^ 8 m/s
宇宙的年龄T =max delta T(life time of universe, 13.799±0.021 billion years) = 4.34 x 10 ^17 s (second)
minon=h-bar/max delta T =( 1.0545718 × 10-34 m2 kg / s)/ 4.34 x 10 ^17 s= 2.429889× 10-52 m2 kg / s2
在此我们称minon为宇宙最小基本能量单元。与此能量对应的最小物质单元质量m0=h-bar/(max delta T*C^2)。我们可以确定现行宇宙的最小能量质量单元能量远比普朗克常数还小很多个数量级(18个数量级)。
我们还提出了在复数空间,引入保形变换1/Z^n,将其点外开放半球变换到点内闭合半球,阴阳平衡,合二为一,从此,宇宙成为有限的统一的整体。这类似于将“柯召-魏时珍猜想”应用于物质的底层,直到宇宙最小能量、最小质量、最小空间单位。
有人质疑这个米农:“以微波背景3k温度作最底层质量单位,你和姜放老师没有考虑微波背景3k温度所涉及的封闭的体积空间。这个温度看似很小,比普朗克低了18个数量级,但是以整个宇宙体积作的背景体积,所以很小。但如果单独使用是非常大的。所以用作底层米农,可以像姜放的基本空间单元一样,就是一个笑话。中科院大学校长官科院士,也在用温度挑战爱因斯坦广义相对论。也许这不成立,道理也如此----少到微观最低温度0度一个量子,就不存在温度概念,即使有运动也如此。因为温度是集体运动的产物。所以龚老师多次来信批评姜放老师的创新,是对的。下面我有龚老师的第2封信。你和姜放老师是学电力和自动化的,对微观单独一个量子或一个电子,在一个有限封闭空间的温度,没有教材讲授过。姜放老师创新出,也不奇怪。罗正大,国家给他出版了9本书,都是自己定义的外力和斥力,不与国家学校的物理教材相同,但自认为可以解决所有物理学难题,他批判引力的所有应用都是错的。近一年多我都在看罗正大的9本书,想我们国家为什么会这样?包括你的美国同学王令隽终身教授,也像罗正大。姜放老师是国内官科的罗正大吗?你想做罗正大吗?”
我们探讨问题,当然,应该质疑!北大校长说:“质疑不能带来。。。。" 。如果连质疑都不要了,还要科学干什么?
有质疑是正常不过的事,也应该予以回复和讨教。我的回答如下:
我所崇尚的物理学:
1,对于宇宙世界必须有一个整体的、全面的、完整的架构;
2,对其中的物理参数、变量有严格的定义,必须有严格的数理逻辑和方程描述;
3,全部假设及其推论,必须最后经过客观事实的严格检验。
以上是物理学而言,更多关于创新理论,何为创新?
4,创新理论,必须接受龚学创新理论定律的检验;
5,创新理论,必须接受龚学完美性10条检验;
6,创新理论,必须接受理论竞争和奥卡姆剃刀原则检验。
我有罗正大的那一堆书,特别是 统一的宇宙,总结了宇宙引力与斥力平衡,探求宇宙的精神值得学习,但其结论都是有待检验的,按以上6点来看,都还需要一一检验验证。
我从来没有联系过,罗大正。虽然,他也是一位值得尊敬的学者兼实业家。我就是我,我不是 罗大正。另外,误会了,我从来没有说过,王令隽先生是我同学。
那么,有人质疑这个米农(minon)理论,我的回答,依据是:
1,宇宙世界是层级结构,标准模型粒子就是宇宙物质的底层了吗?层子结构如何?如中国古人的万世不竭论和毛粒子。 2,龚学理论二元(A,V)描述可计算宇宙与7色描述不可计算宇宙了。但空子数学表达为0,但事实上空子不空,另外还有一代、二代、三代表述、7色结构,是否就是终极了? 3,三旋理论差不多也推进了一层,还形象的描述了各模块的几何结构。完满了吗?
2018-5-8日晚
------------------------------------------------------
这个问题的讨论还在继续:那么,是否可以公开讨论呢?
我不太确定。但我还是将今天回复王老师的信件附上:
2018年5月10日
---------------------------------------------
我们龚学理论指出,引力来自时间。时间驱动宇宙万物从过去、到现在、到未来运动发展。在能量复频域,有规范场对称性,而此规范场对称性的破缺,从复频域转到时间域,按照龚学理论方程0的方式,产生物质粒子和时空,按照统一力方程包括了引力。这个理论将规范场理论、弦论与圈量子、爱因斯坦相对论、量子力学都统一在此架构之中,宇宙万物在龚学看来,已无秘密。 但是否可以更加深入到普朗克常数层底下,这是一次尝试。
因此,这个米农,必定要体现以上原理。
米农理论还在发展之中。
-------------------------------------------------------
龚学理论中,单位时间内每个时间维度的量子行为的数量是{1(/ ħC)}。
因为,宇宙的生命时间,有{1,i, -1, -i} 4个时间维度。因此,这个宇宙的总量子数:
{total Tc总量子作用计数}={1(/ħC)} ^ 4 ×T;
因此,Tc={1(/ħ C)^ 4 } x T= 4.34 /9.714 x 10 ^ 103 x 10 ^ 17
=0.446×10 ^ 120
其中:普朗克常数 ħ=1.0545718×10-34 m2 kg/s
光速C=299 792×458 m/s=2.99×10 ^ 8 m/s。
因此,((ħc)^ 4={(1.05×2.99)x(10 ^(-34+8))}^4=97.14×10 ^(-104)=9.714×10(-103)。
T(宇宙生命周期,13.799±2100万年)=4.34×10 ^ 17秒
到目前为止,这个宇宙应该有一个{总量子行动计数},其数量为10 ^ 120。
龚学理论的宇宙学常数计算:
(Λ) =1/Tc =1 /( 0.446×10 ^ 120 )= = 2.242×10 ^ - 120
宇宙学常数(Λ) 是空间真空能量密度的值。由宇宙常数产生的正真空能量密度意味着负压,反之亦然。在普朗克单位,作为一个自然无量纲值,宇宙学常数,Λ ,是在10 ^ -120的方次。
迄今为止,宇宙学常数(Λ )是一个没有理论表述的现象学参数,尽管它在GR方程中有特指的定义。同样,这个常数还不能被任何主流量子引力理论推导出来。M弦理论甚至不能确定它的符号是正还是负。
如果我们延伸宇宙学常数的定义,为每个米农量子争取一份量子空间、米农量子能量密度。
宇宙学常数(Λ)={宇宙量子能量密度}
= {米农(minon)/现时宇宙米农量子体积(Vm)}
= { 1 / 0.446×10 ^ 120 }
= 2.242×10 ^ - 120
因为:minon=h-bar/max delta T =( 1.0545718 × 10-34 m2 kg / s)/ 4.34 x 10 ^17 s= 2.429889× 10-52 m2 kg / s2
问题:上式计算表明:宇宙学常数层10 ^-120到米农面包圈能量10 ^-52之间有一个10 ^68数量级的巨大鸿沟。
猜测:宇宙初创阶段,经历过一个10^68的白洞的体积膨胀过程,反对称于一个10^68的黑洞的体积收缩(密度增加10 ^ 68)。即minon现时世界的基本单元体积Vm曾经经历过一个10^68的白洞膨胀过程,我们现在看到的minon体积Vm,相对于创世之初体积V0, Vm=V0*10^68,(密度减少10 ^ -68)。
如果没有这个白洞膨胀过程,初始宇宙学常数将比现在高10^68数量级。
从而,现时宇宙学常数(Λ) = {米农(minon)/现时宇宙米农量子体积(Vm)}=
2.242×10 ^ - 120 龚学本身也可以描述这个宇宙膨胀过程:
最新宇宙循环增长周期已经计算出来了!
T=4.34×10^17 秒
N=345
我们的宇宙已经进入了第345个震荡周期。现时宇宙体积:
Rmax=R0*2^345
Vmax(T)=V0*(2^345)^3
-------------------------------------------------------
黑洞、白洞、虫洞
什么是黑洞、白洞、虫洞?他们之间的关系是什么?_宇宙探索_新浪博客 http://blog.sina.com.cn/s/blog_5ea3e1790100co2l.html
什么是黑洞?

什么是白洞?

什么是虫洞?
虫洞可能是连接黑洞和白洞的时空隧道。“虫洞”是连接宇宙遥远区域间的时空细管。它可以把平行宇宙和婴儿宇宙连接起来,并提供时间旅行的可能性。“虫洞”的研究虽然刚刚起步,但是它潜在的回报,不容忽视。科学家认为,如果研究成功,人类可能需要重新估计自己在宇宙中的角色和位置。

白洞、虫洞及虫洞之间的关系
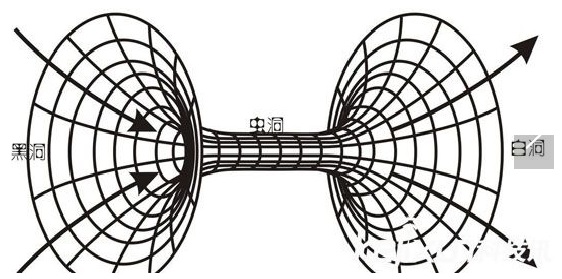
黑洞和黑洞之间也可以通过虫洞连接,当然,这种连接无论是如何的将强,它还是仅仅是一个连通的“宇宙监狱”。虫洞不仅可以作为一个连接洞的工具,它还在宇宙的正常时空中出现,成为一个突然出现在宇宙中的超空间管道。虫洞没有视界,它有的仅仅是一个和外界的分解面。虫洞通过这个分解面和超空间连接,但是在这里时空曲率不是无限大。就好比在一个在平面中一条曲线和另一条曲线相切,在虫洞的问题中,它就好比是一个四维管道和一个三维的空间相切,在这里时空曲率不是无限大。
以上是现有科普版的白洞、黑洞、及虫洞理论,兼容于米农理论。
这个宇宙学常数完全是整个宇宙量子总数10 ^ 120 的倒数。采用保形变换1/Z^n, n可取{1,0,-1,} 将宇宙整体反对称映射,包括巨大的黑洞与白洞的反对称与镜对称,直达宇宙的最底层—-宇宙学常数层。反之亦然。
米农就是附着在10^68之白洞表面的最小能量面包圈量子。或可以看作SYZ镜对称或T对偶性之四维卡拉比-丘流形上的K3环面或环圈。
以上龚学理论中的宇宙学常数的引入,以及黑洞、白洞、虫洞的引入,更能说明宇宙的底线宇宙量子的 能量密度为 10 ^ – 120数量级的含义。而且,进一步表明龚学循环多宇宙,正负黑白宇宙之转换演变。
这个演变过程在数学上已经有“庞加莱猜想外定理”, 还有 上面文章提到的“柯召-魏时珍猜想”的支持。
————————————————————————-
2017年-2018年,本人注意到汪一平先生发展的相对论圆对数理论。我认为,可以用圆对数理论来描述最大宇宙、中观宇宙(基本粒子宇宙)、最小宇宙之间的关系。这个想法得到汪一平先生的赞赏与支持,在此表示感谢。
汪一平圆对数有:(y = xz)。它是与传统分析方法不同的“(B-R)理论”。该方法采用由1763年英国贝叶斯(B)(1702—1763)与1982年中国汪一平(R或RELH)(1937—)各自独立提出相似的(相对度—相对性结构)原理,可以并成为一种新的数学分析方法(y = xz),称其为(B-R)理论。数学特征:“既定的数值用相对可变的底数f(x)= (1-η2) z x 0 自乘一个相对不变的幂次、指数函数(z=ck),建立相对性原理,由此建立了f(x)的底数函数形式,成为的相对性结构原理,其中:
y = xz = [(1-η2) z x0 ]
有:
η = ∑(ηi)(标量);
(或):
幂指数:
η = Cηh; C = ∑Ci; C:路径积分值,
零点值:(1-η2) = (0,(1/2),1,2)= (0,(1/2)k);
η =(C)ηh
式中:(x)可变底数,(x0)底数算术平均值。(1-η2)c中,η =(Cηh)为相对性结构因子与路径积分一致性;ηh:为相对性标准量,可转化为相对性结构因子;C:幂次流,它可以是级数、超越函数、多项式等形式,籍此处理了多层(高维)次与低层(维)次的统一关系,并使其函数由积(除)转化为和(差),最后在边界处给予重整化为相对不变值。
这样一来,(B-R)理论很好地处理了把复杂的非线性函数(f(x))兼并为简单多项式的非线性函数(1-η2)z,再转化为简单的线性函数(η)的计算分析。这意味着自然界规律错综复杂的变化,大多都可归纳为简单的线性变化规律,而错综复杂的根源在于不同元素在不同的区域有其不同个性的作用“参数”,一旦用相对性理论剔除了个性,剩下了具共性的、统一的自然定律。这点或许有对传统观念很深感情的人认为“没有那么简单”,“不好相信”。但是,中国有句名言 “实践检验真理”。可参考汪一平博客文章全部内容,说明了用(B-R)理论很好地处理了若干个世界著名难题以及形形色色各种类型的应用实例。
汪一平先生对米农理论的点评:
1.甚至米农本身还可以是一个圈量子,当然,简单起见,球粒子也可以,但加上一元扩展成复数,一旋(圆对数进动方程),二旋(圆对数电磁理论)、三旋(圆对数自旋加进动方程),满足8周期律,64周期律,【一直到{2}^KN】(这里需要数学证明,组合同构性及以{2}^KN,[K=+1,0,-1]的跨越)即【P=NP完全问题】
24,以上迭代,直到普朗克层、基本粒子层、宏观物质层(龚学思想没错) 。【一直到整个宇宙】(这里需需要单一化或量粒子化证明)【霍奇猜想、抽象庞加莱猜想】。
2. 龚学理论指出,引力【各种质能(场)、性质(正中反三态)、极限(层次)的变化】均来【自对时间的假设与作用】需要【黎曼猜想、BSD猜想】。杨振宁规范场包含运动方程、电磁方程(K=-1)、元素组合概念,独缺引力(K=+1)的描述,关键点是“要求没有质量具体元素的数学四则运算”。这是当前的前沿课题。我可能先走了一步,还不敢说‘建立完整性的数学基础’。
3. 上述全球华人的三个理论,我认为基本上都没有冲突,但在数学的定量证明(或量化计算)都不能说【具有完整性】。一旦提取它们的变化共性,摆脱具体的质量元素的干扰,方便的给于数学完整性证明,就成为圆对数概念。但是依然采用“传统(有限)微积分方法,不能解决(无穷元素与无限组合)的完全问题”。我很希望李教授能够把中国上述学者的优点集合起来,拓展成为具有新颖性的数学物理理论。
参见:探索自由天空_新浪博客 http://blog.sina.com.cn/lkx0570
137、“(B-R)理论”或将挑战“数学理论”在于作出实质性进步_探索自由天空_新浪博客 http://blog.sina.com.cn/s/blog_618a0bbf01017fow.html
2018-5-16
————————————————————————-
讨论还将继续。
—————————————————————————
我们的结论:最大宇宙与最小宇宙是一个数学上反对称的平衡统一的系统。
赞龚学—米农量子—-宇宙学常数
神龙只见尾,龙首在云端。云深不可测,盘旋入空无。
5-20修改加韵:
神龙只见尾,龙首在云中。云深不可测,盘旋入虚空。
———————————————————————–
吴岳良院士的引力量子场理论:
-
引力量子场论
引力量子场论_百度百科 https://baike.baidu.com/item/%E5%BC%95%E5%8A%9B%E9%87%8F%E5%AD%90%E5%9C%BA%E8%AE%BA/19311379?fr=aladdin
- 中文名
- 引力量子场论
- 外文名
- Gravitational Quantum Field Theory
- 提出者
- 吴岳良
- 提出时间
- 2016年
基本概述
提出动机
建立基础
基本假设和原理
基本性质和研究内容
(1)基本引力场是定义在局域平坦非坐标四维时空和整体平坦四维闵氏坐标时空的双协变矢量场
(X)。 这里的矢量场
(X)是伴随基本粒子量子场具有局域自旋规范对称性SP(1,3) 和标度规范对称性时而引入的双协变矢量场,其对偶场 耦合到所有量子场的动力学项和规范相互作用项;
In a paper posted online last fall, mathematicians Mihalis Dafermos and Jonathan Luk have proven that the strong cosmic censorship conjecture, which concerns the strange inner workings of black holes, is false.
“I personally view this work as a tremendous achievement — a qualitative jump in our understanding of general relativity,” emailed Igor Rodnianski, a mathematician at Princeton University.
The strong cosmic censorship conjecture was proposed in 1979 by the influential physicist Roger Penrose. It was meant as a way out of a trap. For decades, Albert Einstein’s theory of general relativity had reigned as the best scientific description of large-scale phenomena in the universe. Yet mathematical advances in the 1960s showed that Einstein’s equations lapsed into troubling inconsistencies when applied to black holes. Penrose believed that if his strong cosmic censorship conjecture were true, this lack of predictability could be disregarded as a mathematical novelty rather than as a sincere statement about the physical world.
“Penrose came up with a conjecture that basically tried to wish this bad behavior away,” said Dafermos, a mathematician at Princeton University.
This new work dashes Penrose’s dream. At the same time, it fulfills his ambition by other means, showing that his intuition about the physics inside black holes was correct, just not for the reason he suspected.
Relativity’s Cardinal Sin
In classical physics, the universe is predictable: If you know the laws that govern a physical system and you know its initial state, you should be able to track its evolution indefinitely far into the future. The dictum holds true whether you’re using Newton’s laws to predict the future position of a billiard ball, Maxwell’s equations to describe an electromagnetic field, or Einstein’s theory of general relativity to predict the evolution of the shape of space-time. “This is the basic principle of all classical physics going back to Newtonian mechanics,” said Demetrios Christodoulou, a mathematician at ETH Zurich and a leading figure in the study of Einstein’s equations. “You can determine evolution from initial data.”
But in the 1960s mathematicians found a physical scenario in which Einstein’s field equations — which form the core of his theory of general relativity — cease to describe a predictable universe. Mathematicians and physicists noticed that something went wrong when they modeled the evolution of space-time inside a rotating black hole.
To understand what went wrong, imagine falling into the black hole yourself. First you cross the event horizon, the point of no return (though to you it looks just like ordinary space). Here Einstein’s equations still work as they should, providing a single, deterministic forecast for how space-time will evolve into the future.

Lucy Reading-Ikkanda/Quanta Magazine
But as you continue to travel into the black hole, eventually you pass another horizon, known as the Cauchy horizon. Here things get screwy. Einstein’s equations start to report that many different configurations of space-time could unfold. They’re all different, yet they all satisfy the equations. The theory cannot tell us which option is true. For a physical theory, it’s a cardinal sin.
“The loss of predictability that we seem to find in general relativity was very disturbing,” said Eric Poisson, a physicist at the University of Guelph in Canada.
Roger Penrose proposed the strong cosmic censorship conjecture to restore predictability to Einstein’s equations. The conjecture says that the Cauchy horizon is a figment of mathematical thought. It might exist in an idealized scenario where the universe contains nothing but a single rotating black hole, but it can’t exist in any real sense.
The reason, Penrose argued, is that the Cauchy horizon is unstable. He said that any passing gravitational waves should collapse the Cauchy horizon into a singularity — a region of infinite density that rips space-time apart. Because the actual universe is rippled with these waves, a Cauchy horizon should never occur in the wild.
As a result, it’s nonsensical to ask what happens to space-time beyond the Cauchy horizon because space-time, as it’s regarded within the theory of general relativity, no longer exists. “This gives one a way out of this philosophical conundrum,” said Dafermos.
This new work shows, however, that the boundary of space-time established at the Cauchy horizon is less singular than Penrose had imagined.
To Save a Black Hole
Dafermos and Luk, a mathematician at Stanford University, proved that the situation at the Cauchy horizon is not quite so simple. Their work is subtle — a refutation of Penrose’s original statement of the strong cosmic censorship conjecture, but not a complete denial of its spirit.
Building on methods established a decade ago by Christodoulou, who was Dafermos’s adviser in graduate school, the pair showed that the Cauchy horizon can indeed form a singularity, but not the kind Penrose anticipated. The singularity in Dafermos and Luk’s work is milder than Penrose’s — they find a weak “light-like” singularity where he had expected a strong “space-like” singularity. This weaker form of singularity exerts a pull on the fabric of space-time but doesn’t sunder it. “Our theorem implies that observers crossing the Cauchy horizon are not torn apart by tidal forces. They may feel a pinch, but they are not torn apart,” said Dafermos in an email.
Because the singularity that forms at the Cauchy horizon is in fact milder than predicted by the strong cosmic censorship conjecture, the theory of general relativity is not immediately excused from considering what happens inside. “It still makes sense to define the Cauchy horizon because one can, if one wishes, continuously extend the space-time beyond it,” said Harvey Reall, a physicist at the University of Cambridge.
Dafermos and Luk prove that space-time extends beyond the Cauchy horizon. They also prove that from the same starting point, it can extend in any number of ways: Past the horizon “there are many such extensions that one could entertain, and there is no good reason to prefer one to the other,” said Dafermos.
Yet — and here’s the subtlety in their work — these nonunique extensions of space-time don’t mean that Einstein’s equations go haywire beyond the horizon.
Einstein’s equations work by quantifying how space-time changes over time. In mathematical language, it takes derivatives of an initial configuration of space-time. In order for it to be possible to take a derivative, space-time has to be sufficiently “smooth” — free of discontinuous jumps. Dafermos and Luk indicate that while space-time exists beyond the Cauchy horizon, this extended space-time isn’t smooth enough to actually satisfy Einstein’s equations. Thus, even with the strong cosmic censorship proven false, the equations are still spared the ignominy of outputting nonunique solutions.
“It makes sense to talk of the Cauchy horizon; however, you can’t continue beyond it as a solution of Einstein’s equations,” said Reall. “They’ve offered pretty convincing evidence that that is true, in my opinion.”
You could think of this outcome as a disappointing compromise: Even though you can extend space-time beyond the Cauchy horizon, Einstein’s equations can’t be solved. But it’s precisely the fact that this middle ground seems to exist that makes Dafermos and Luk’s work so interesting.
“This is people really discovering a new phenomenon in the Einstein equations,” said Rodnianski.
Correction: This article was updated on May 18, 2018, to reflect that it has been 40 years since Roger Penrose proposed the strong cosmic censorship conjecture, not 60 years.
2018年5月19日,李小坚 转自量子杂志
—————————————-
物质世界微观和宏观的区别
所有学科的微观和宏观都是一个相对的概念。数量级就是对这个概念的一个具体描述。既相差十倍以上就不是一个数量级的事物了。当然即便是相差几个数量级,微观的效果依然会反应到宏观的范畴,只是不起决定性作用或者可以忽略其存在而已。
但是量子力学的微观和宏观还有更明确的区分条件。这个条件就是量子力学的空间概念和四维时空的空间概念是不同的。
所以量子力学不能描述四维时空中的物质运动。同时四维时空中也看不见量子力学描述的大部分概念。既四维时空是由物质的黎曼维度形成,而量子力学的维度是物质的复辛维度。所以两者之间的区别是非常明显的,而联系则是更高一级的数学关系。
所以在物质世界微观和宏观之间就存在一条鸿沟。区别微观和宏观的方法也是这条鸿沟。
既符合黎曼代数关系的维度就是宏观关系。
而相互之间符合复辛代数关系的维度之间就是微观。
这个原理不仅适应物质世界,也适应其它的学科。





