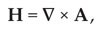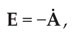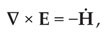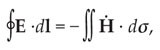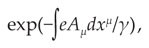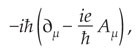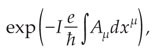2018 新年伊始, 物理学泰斗杨振宁先生就开场布道了!
于2018年元月3日下午4点,在国家天文台学术交流委员会举行了一场报告—-新年专场:
杨振宁先生: 麦克斯韦方程与规范理论的起源
http://view.inews.qq.com/a/KEP2017121802038600
 对这个报告,腾讯视频进行了现场直播。报告现场气氛热烈。杨振宁先生不仅回顾了电磁场理论的发展历史,解释了规范场论的形成的过程,直到标准模型的伟大成就,并认为LHC发现的Higgs玻色子为SM完成最后的验证,似乎为SM画上完满的句号。
对这个报告,腾讯视频进行了现场直播。报告现场气氛热烈。杨振宁先生不仅回顾了电磁场理论的发展历史,解释了规范场论的形成的过程,直到标准模型的伟大成就,并认为LHC发现的Higgs玻色子为SM完成最后的验证,似乎为SM画上完满的句号。
这些工作对中国年轻人还是很有启发意义,特别是他回答年轻人提出的问题有很大的指导意义且很有针对性,相当精彩!这个报告对中国物理界也有很大的引领与启示作用。
现代物理学是人类最伟大的成就,而杨振宁先生是当代最伟大的物理学家。他的贡献不亚于爱因斯坦、泡利、温伯格等其他诺贝尔奖获得者。因为他参与了现代物理学形成的这个进程,并作出了个人的努力和杰出贡献。因此,他对现代物理是什么有极好的理解。
现代物理学有两个分支:现代经典理论和当代龚学理论。杨振宁先生是前一个分支达到顶峰的代表人物。杨先生关于历史的渊源对话中确切地显示了物理学应该是什么。当然,大多数正在学习与成长的年轻物理学家不会透彻理解杨先生所有的观点。
传统物理学的认识论是根据现象学获得的实验数据,利用数学理论加以抽象描述成基本方程。也就是说,数学只是传统物理学的一种工具或一种语言,而杨先生将数学列为与物理同样揭示宇宙世界的基本方法。杨振宁先生的高明之处,还在于努力探寻现象背后的抽象物理数学原理的实质问题。这些工作充分发挥了杨振宁先生的数学长处,但似乎缺失一点哲学高度!当然,所有的物理学抽象原理都有一个底线:必须接受自然世界最后的判断;也就说,如果不符合自然客观,再漂亮的数学或高深的哲学都不能在物理学中起任何作用。
龚学理论是现代物理学的最高成就。龚学认识论给出一种哲学高度的第一原理为基础,采用预定设计的公理和定义,构建了一个虚构的宇宙系统FU。然后,FU与自然客观世界的现实结果进行比较。
同样,FU必须接受自然世界最终裁判。任何不符合这个最终裁判的理论只能是垃圾,并被历史扬弃。
关键是龚学理论恰恰满足现代物理客观观测的所有重要结果,而且,未来还有很多物理观测数据的出现,还会进一步证实龚学理论必然与这个客观世界的观测结果相一致。
如:1)未来几年LHC 对HIGGS粒子进一步认识,将会发现该玻色子是龚学的真空子。2) 未来几年LIGO及其量子引力研究,将会证明龚学的统一力方程的正确无误。3)未来数学纤维丛结构、天体物理学观测以及CKM精密测量等验证将揭示龚弦宇宙的结构的精妙,而这个精妙结构的龚学计算早已经摆在那里。
我们预测,这些工作将在十年内得到完全的验证。(这样的预测在两年前就已做出。因此,严格意义上说:在未来八年内,以上工作将得到完全的验证)。从而显示,龚学理论将引领现代物理学的发展。
附:
2014年6月,杨振宁先生在新加坡举办的第8届全球华人物理学家大会上所作的类似的报告:
——————————————————–
The conceptual origins of Maxwell’s equations and gauge theory
Chen Ning Yang
Already in Faraday’s electrotonic state and Maxwell’s vector potential, gauge freedom was an unavoidable presence. Converting that presence to the symmetry principle that underpins our successful standard model is a story worth telling.
It is often said that after Charles Augustin de Coulomb, Carl Friedrich Gauss, AndréMarie Ampère, and Michael Faraday discovered the four experimental lawsconcerning electricity and magnetism, James Clerk Maxwell added the displacement current and thereby created the great set of Maxwell’s equations.That view is not entirely wrong, but it obscures the subtle interplay betweensophisticated geometrical and physical intuitions that led not only to thereplacement of “action at a distance” by field theory in the 19th century butalso, in the 20th century, to the very successful standard model of particle physics.
In 1820 Hans Christian Oersted (1777–1851) discovered that an electric current would always cause magnetic needles in its neighborhood to move. The discovery electrified the whole of Europe and led to the successful mathematical theoryof “action at a distance” by Ampère (1775–1836). In England, Faraday(1791–1867) was also greatly excited by Oersted’s discovery. But he lacked the mathematical training needed to understand Ampère. In a letter to Ampère dated 3 September 1822, Faraday lamented, “I am unfortunate in a want of mathematical knowledge and the power of entering with facility into abstract reasoning. I am obliged to feel my way by facts closely placed together.” 1
Faraday’s “facts” were his experiments, both published and unpublished. During a period of 23 years, 1831–54, he compiled the results of those experiments into three volumes, called Experimental Researches in Electricity, which we shall refer to as ER (figure 1). A most remarkable thing is that there was not a single formula in this monumental compilation, which showed that Faraday was feeling his way, guided only by geometric intuition without any precise algebraic formulation.
Figure 1. Three volumes of Faraday’s Experimental Researches in Electricity, published separately in 1839, 1844, and 1855. On the right is the first page of the first volume.
Figure 2 shows a diagram from Faraday’s diary, dated 17 October 1831, the day he found that moving a bar magnet either into or out of a solenoid would generate electric currents in the solenoid.Thus he had discovered electric induction, which, as we know, eventually led to making big and small generators of electricity and thereby changed the technological history of mankind.
Figure 2. Michael Faraday in an etched portrait. The inset shows the diagram Faraday drew in his diary on 17 October 1831, the day he discovered induction.
Throughout the volumes of ER, Faraday explored variations of his induction experiment: He changed the metal used for winding the solenoid, immersed the solenoid in various media, created induction between two coils, and so on. He was especially impressed by two facts—namely, that the magnet must be moved to produce induction, and that induction seemed to produce effects perpendicular to the cause.
Feeling his way toward an understanding of induction, he introduced two geometric concepts: magnetic lines of force and the electrotonic state. The former was easily visualized by sprinkling iron filings around magnets and solenoids.Those lines of force are today designated by the symbol H, the magnetic field. The latter, the electrotonic state, remained indefinite and elusive throughout the entire ER. It first appeared early involume 1, section 60, without any precise definition. Later it was variously called the peculiar state, state of tension, peculiar condition, and other things. For example, in section 66 he wrote, “All metals take on the peculiar state,” and in section 68, “The state appears to be instantly assumed.” More extensively, we read in section 1114,
If we endeavour to consider electricity and magnetism as the results of two faces of a physical agent, or a peculiar condition of matter, exerted in determinate directions perpendicular to each other, then, it appears to me, that we must consider these two states or forces as convertible into each other in a greater or smaller degree.
When Faraday ceased his compilation of ER in 1854 at age 63, his geometric intuition, the electrotonic state, remained undefined and elusive.
Maxwell
Also in1854, Maxwell (1831–79) graduated from Trinity College. He was 23 years old and full of youthful enthusiasm. On February 20 he wrote to William Thomson,
Suppose a man to have a popular knowledge of electric show experiments and a little antipathy to Murphy’s Electricity, how ought he to proceed in reading & working so as to get a little insight into the subject wh[sic] may be of use infurther reading?
If he wished to read Ampere Faraday &c how should they be arranged, and at what stage & in what order might he read your articles in the Cambridge Journal? 2
Thomson (later Lord Kelvin, 1824–1907) was a prodigy. At the time, he had already occupied the Chair of Natural Philosophy at Glasgow University for eight years.Maxwell had chosen well: Earlier in 1851 Thomson had introduced what we nowcall the vector potential A to express the magnetic field H through
an equation that would be of crucial importance for Maxwell, as we shall see.
We do not know how Thomson responded to Maxwell’s inquiry. What we do know is that, amazingly, only a little more than one year later, Maxwell was able to use equation (1) to give meaning to Faraday’selusive electrotonic state and publish the first of his three great papers,which revolutionized physics and forever changed human history. Those three papers together with others by Maxwell had been edited by William Davidson Nivenin 1890 into a two-volume collection, Scientific Papers of JamesClerk Maxwell, which we shall refer to as JM.
Maxwell’s first paper, published in 1856, is full of formulas and therefore easier to read than Faraday’s ER. Its central ideas are contained in part 2,which has as its title “Faraday’s Electro-tonic State.” On page 204 in this part 2 we find an equation that in today’s vector notation is
where A is Faraday’s electrotonic intensity.
Three pages later, on page 207 of JM, the result is restated inwords:
Law VI. The electro-motive force on any element of a conductor is measured by the instantaneous rate of change of the electro-tonic intensity on that element, whether in magnitude or direction.
The identification of Faraday’s elusive idea of the electrotonic state (or electrotonic intensity, or electrotonic function) with Thomson’s vector potential A defined in equation (1) above is, in my opinion, the first great conceptual breakthrough in Maxwell’s scientific research: Taking the curl of both sides of equation (2) we obtain
which is the modern form of Faraday’s law. Another modern form of it is
where d l is a line element and d σ is an element of area. Maxwell did not write Faraday’s law in either of the two forms in equations (3) and (4) because his aim was to give precise definition to Faraday’s elusive concept of the electrotonic state. Indeed, the concept of the vector potential A remained central in Maxwell’s thinking throughout his life.
Maxwell was aware of what we now call the gauge freedom in equations 1–3, namely, that the gradient of an arbitrary scalar function can be added to A without changing the result. He discussed that freedom explicitly in theorem 5 on page 198 of JM. So which gauge did he choosefor A in equations 1–3? He did not touch on that question, but left it completely indeterminate. My conclusion: Maxwell implied that there exists a gauge for A in which equations 1–3 are satisfied.
Maxwell was also fully aware of the importance of his identification of Faraday’selectrotonic intensity with Thomson’s A. He was afraid that Thomson might take offense concerning the priority question. He therefore concluded part 2 of his first paper with the following remark:
With respect to the history of the present theory, I may state that the recognitionof certain mathematical functions as expressing the “electro-tonic state” of Faraday, and the use of them in determining electro-dynamic potentials and electro-motive forces is, as far as I am aware, original; but the distinct conception of the possibility of the mathematical expressions arose in my mind from the perusal of Prof. W. Thomson’s papers. ( JM, page 209)
Maxwell’s vortices
Five years after completing his first paper, Maxwell began publishing his second, which appeared in four parts during 1861 and 1862. In contrast to the earlier paper, the second is very difficult to read. The main idea of the paper was to account for electromagnetic phenomena “on the hypothesis of the magnetic field being occupied with innumerable vortices of revolving matter, their axes coinciding with the direction of the magnetic force at every point of the field,” as we read in JM on page 489.
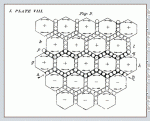
Maxwell gave an explicit example of such an intricate group of vortices in a diagram reproduced here as figure 3 , which he explained in detailon page 477 of JM in the following passage:
Figure 3. A figure of vortices from a plate in the 1890 collection Scientific Papers of James Clerk Maxwell, facing page 488. The directions of the arrows in two of the hexagonal vortices in the second row from the bottom are incorrect, presumably mistakes of Maxwell’s draftsman.
Let AB, Plate VIII., p. 488, fig. 2, represent a current of electricityin the direction from Ato B. Let the large spaces above and below AB represent the vortices, and let the small circles separating the vortices represent the layers of particles placed between them, which in our hypothesis represent electricity.
Now let an electric current from left to right commence in AB. The row of vortices ghabove AB will be set in motion in the opposite direction to that of a watch. (We shall call this direction +, and that of a watch –.) We shall suppose the row of vortices kl still at rest, then the layer of particles between these rows will be acted on by the row gh on their lower sides, and will be at rest above. If they are free to move, they will rotate in the negative direction, and will at the same time move from right to left, or in the opposite direction from the current, and so form an induced electric current.
That detailed explanation of Maxwell’s model appeared in part 2 of his second paperand was published in Philosophical Magazine, volume 21, April–May 1861. Maxwell evidently took his intricate network of vortices very seriously and devoted the remaining 11 pages of part 2 to detailed studies of the model.
Then in January and February 1862, Maxwell published part 3 of his second paper withthe title, “The Theory of Molecular Vortices Applied to Statical Electricity.” Seven pages of analysis led to his proposition 14: “To correct the equations ofelectric currents for the effect due to the elasticity of the medium” ( JM, page 496). The correction was to add a “displacement current” Ė to Ampère’s law, which in modern notation then reads ∇ × H = 4 π j + Ė.
I had made several attempts to read the last 11 pages of part 2 and the first 7 pages of part 3, trying to see how Maxwell was led to his correction. In particular, I wanted to learn what he meant by “the effect due to the elasticity of the medium.” All my attempts failed. It is noteworthy that in the last 11 pages ofpart 2, the word “displacement” occurs only once, on page 479, in an unimportant sentence, whereas in the beginning 7 pages of part 3 that word becomes the center of Maxwell’s focus. Thus it seems that in the eight months between the publication of the two parts, Maxwell had found new features of his network of vortices to explore, leading to the displacement current.
After proposition 14 Maxwell quickly concluded that there should be electromagnetic waves. He calculated their velocity, compared it with the known velocity of light, and reached the momentous conclusion that “We can scarcely avoid the inference that light consists in the transverse undulations of the same medium which is the cause of electric and magnetic phenomena” (page 500; the italics are Maxwell’s).
Maxwell was a religious person. I wonder whether after this momentous discovery he had in his prayers asked for God’s forgiveness for revealing one of His greatest secrets.
The birth of field theory
Maxwell’s third paper, published in 1865, gave rise to what today we call Maxwell’s equations, of which there are four in vector notation. Maxwell used 20 equations: He wrote them in component form and also included equations for dielectrics and electric currents.
That third paper is historically the first to give a clear enunciation of the conceptual basis of field theory—that energy resides in the field:
In speaking of the Energy of the field, however, I wish to be understood literally. All energy is the same as mechanical energy, whether it exists in the form of motion or in that of elasticity, or in any other form. The energy in electromagnetic phenomena is mechanical energy. The only question is, Where does it reside? On the old theories it resides in the electrified bodies,conducting circuits, and magnets, in the form of an unknown quality called potential energy, or the power of producing certain effects at a distance. On our theory it resides in the electromagnetic field, in the space surrounding the electrified and magnetic bodies, as well as in those bodies themselves, and is in two different forms, which may be described without hypothesis as magnetic polarization and electric polarization, or, according to a very probable hypothesis, as the motion and the strain of one and the same medium. ( JM, page 564)
But, inconformity with the prevalent ideas of the time, Maxwell also wrote,
We have therefore some reason to believe, from the phenomena of light and heat, that there is an aethereal medium filling space and permeating bodies, capable of being set in motion and of transmitting that motion from one part to another,and of communicating that motion to gross matter so as to heat it and affect it in various ways. ( JM, page 528)
Maxwell realized the great importance of his discovery of the displacement current and his conclusion that light is electromagnetic waves. In his third paper, he collected the formulas of the two earlier papers and listed them together. In the process he must have reviewed the arguments that had led to those formulas. So after his review, how did he feel about the intricate network of vortices that had led to the displacement current three years earlier? Maxwell did not discuss that point. But we notice that the word “vortex” did not appear in any of the 71 pages of his third paper. It thus seems reasonable to assume that in 1865 Maxwell no longer considered as relevant the network of vortices of hissecond paper. But he still saw the necessity of “an aethereal medium filling spaceand permeating bodies.”
In 1886 Heinrich Hertz (1857–94) experimentally verified an important consequence of Maxwell’s equations: that electromagnetic waves can be generated by one set of electric circuits and detected by another.
Starting in the mid 1880s Oliver Heaviside (1850–1925) and Hertz independently discovered that one can eliminate from Maxwell’s equations the vector potential A. The simplified equations then have the additional attractive feature of exhibiting a high degree of symmetry between the electric and magnetic fields. We now know that in quantum mechanics, the vector potential cannot be eliminated. It has observable effects as in the Aharonov–Bohm effect.
Into the 20th century
A conceptual revolution in field theory came early in the 20th century following Albert Einstein’s 1905 special theory of relativity, which asserted that there is no other medium at all: The electromagnetic field is the medium. The vacuum is then the state of a region of spacetime where there is no electromagnetic radiation and no material particles. That solved the puzzle posed by the 1887 Michelson–Morley experiment, which looked for the aethereal medium but failed to find it. Most physicists today believe Einstein’s motivation in formulating the theory of special relativity was not to solve the puzzle posed by the Michelson–Morley experiment but rather to recognize the correct meaning of the concept of simultaneity.
In the years 1930–32, with the experimental discovery of the positron, it became necessary to drastically modify one’s view of the vacuum and to adopt instead Paul Dirac’s theory of the infinite sea of negative-energy particles. That was another conceptual revolution in field theory, and it culminated in the theory of quantum electrodynamics. QED proved successful for low-order calculations in the 1930s but was beset with infinity-related difficulties in calculations carried out to higher orders.
In a series of brilliant and dramatic experimental and theoretical breakthroughs in the 1947–50 period, QED became quantitatively successful through the method of renormalization—a recipe for calculating high-order corrections. The latest report of the calculated value of the anomalous magnetic moment of the electron, 3 a = ( g − 2)/2, is in agreement withits experimental value to an incredible accuracy of one part in 10 9 (see the Quick Study by Gerald Gabrielse, Physics Today, December 2013, page64).
With the success of the renormalization program of QED and with the experimental discovery of many mesons and strange particles, efforts were made to extend field theory to describe the interactions between all of the new particles. Papers and books appeared on scalar meson theory with vector interaction, pseudoscalar meson theory with pseudoscalar interaction, and other esoteric topics. None of those efforts produced fundamental advances in our conceptual understanding of interactions. There were also enthusiastic supporters of efforts to find alternatives to field theory, but again no real breakthroughs.
Return to field theory
In the1970s physicists returned to field theory, specifically to non-abelian gauge theory, which was an elegant generalization of Maxwell’s theory. The term non-abelian means that the order in which rotations or other operations take place matters. (I discussed gauge theories and other things in “Einstein’s impact on theoretical physics,” Physics Today, June 1980, page 42.For a more technical discussion, see the article by Isidore Singer, PhysicsToday, March 1982, page 41.) Gauge theory is today recognized as of fundamental conceptual importance in the structure of interactions in the physical universe. It started with three papers published in 1918–19 by mathematician Hermann Weyl, who was influencedby Einstein’s call for the geometrization of electromagnetism. 4
Weyl was motivated by the importance of parallel displacement. He argued that “the fundamental conception on which the development of Riemann’s geometry must be based if it is to be in agreement with nature, is that of the infinitesimal parallel displacement of a vector.” Weyl then said that if, in the infinitesimal displacement of a vector, its direction keeps changing, then “Warum nicht auch seine Länge?” (Why not also its length?) Thus Weyl proposed a nonintegrable “Strecken facktor,” or “Proportionalitäts facktor,” which here lated to the electromagnetic field through
in which A μ is the four-dimensional vector potential and the coefficient γ is real. Weyl attached such a stretch factor to every charged object moving through spacetime. To the second of Weyl’s three papers, Einstein appended a postscript that criticized Weyl’s idea of length changes indisplacements. Weyl was unable to effectively respond to this devastating criticism.
After the development of quantum mechanics in 1925–26, Vladimir Fock and Fritz London independently pointed out that in the new quantum framework, it was necessaryto replace ( p – e A) by
which suggested the replacement in equation (5) of eA μdx μ / γ by ieA μdx μ / ħ, that is, of γ by − iħ.
Evidently, Weyl accepted the idea that γ should be imaginary, and in1929 he published an important paper in which he explicitly defined the concept of gauge transformation in QED and showed that under such a transformation, Maxwell’s theory in quantum mechanics is invariant.
Under a gauge transformation, Weyl’s length-change factor is replaced by
which evidently should have been called a phase-change factor. The replacement also renders inoperative Einstein’s criticism of Weyl’s idea mentioned above.
That Maxwell’s equations have a high degree of symmetry was first shown in 1905–07 by Einstein and Hermann Minkowski, who separately discovered the equations’ Lorentz invariance. Weyl’s 1929 discovery that Maxwell’s equations are invariant under gauge transformations revealed another symmetry property of the equations. Today we realize that these symmetry properties make Maxwell’sequations a fundamental pillar in the structure of the physical universe.
Weyl’s gauge transformation involves, at every spacetime point, a so-called U(1) rotation—essentially a simple rotation in the complex plane. There is thus a striking similarity between Weyl’s gauge transformation and Maxwell’s network of rotating vortices. The similarity is, of course, fortuitous.
Mathematically, the phase factors of formula 7 form a Lie group U(1), and one of Weyl’s favorite research fields was Lie groups. Going one step further for the more technical reader, had fiber-bundle theory been developed before 1929, Weyl could certainly have realized that electromagnetism was a U(1) bundle theory and would likely have generalized it to non-abelian gauge theory as a natural mathematical extension in 1929.
In the event, the extension was made in 1954, motivated not by mathematical considerations but by the need to find a principle for interactions in the new field of particle physics in which there were found many new “strange” particles. The physical motivation was concisely stated in a short 1954 abstract:
The electric charge serves as a source of electromagnetic field; an important concept in this case is gauge invariance which is closely connected with (1) the equation of motion of the electromagnetic field, (2) the existence of a current density, and (3) the possible interactions between a charged field and the electromagnetic field. We have tried to generalize this concept of gauge invariance to apply to isotopic spin conservation. 5
That extension led to a non-abelian field theory that was very beautiful but was not embraced by the physics community for many years because it seemed to require the existence of massless charged particles.
To give mass to the massless particles in a non-abelian field theory, the concept of spontaneous symmetry breaking was introduced in the 1960s. That concept in turn led to a series of major advances, and finally to a U(1) × SU(2) × SU(3) gauge theory of electroweak interactions and strong interactions that we now call the standard model. In the fifty-some years since 1960, the international theoretical and experimental research community working in “particles and fields” combined their individual and collective efforts to develop and verify the standard model. Those efforts met with spectacular success, climaxing in the discovery of the Higgs boson in 2012 by two large experimental groups at CERN, each consisting of several thousand physicists (see Physics Today, September 2012,page 12).
Despite its impressive success, the standard model is not the final story. To start with, dozens of constants need to enter the model. More important, one of its chief ingredients, the symmetry-breaking mechanism, is a phenomenological construct that in many respects is similar to Fermi’s proposed “four- ψ interaction” to explain beta decay. 6 That 1934 theory was also successful for almost 40 years. But it was finally replaced by the deeper U(1) × SU(2) electroweak theory.
Gauge freedom was explicitly known to Thomson and Maxwell in the 1850s. It probably had also been vaguely sensed by Faraday in his elusive formulation of the electrotonic state. The gauge freedom was converted by Weyl in 1929 to a symmetry (or invariant) property of Maxwell’s equations in quantum mechanics.That symmetry property, now called gauge symmetry, forms the structural backbone of the standard model today.
Maxwell’sequations are linear. In non-abelian gauge theory, the equations are nonlinear. The nonlinearity arises conceptually from the same origin as the nonlinearityof the equations of general relativity. About the latter nonlinearity Einsteinhad written,
We shall speak only of the equations of the pure gravitational field.
The peculiarity of these equations lies, on the one hand, in their complicated construction, especially their non-linear character as regards the field-variables and their derivatives, and, on the other hand, in the almost compelling necessity with which the transformation-group determines this complicated field-law. (reference 7 , page 75)
The true laws can not be linear nor can they be derived from such. (page 89)
Entirely independent of developments in physics, there emerged during the first half of the 20th century a mathematical theory called fiber-bundle theory, which had diverse conceptual origins, including differential forms (mainly due to élie Cartan), statistics (Harold Hotelling), topology (Hassler Whitney), global differential geometry (Shiing-Shen Chern), and connection theory (Charles Ehresmann). The great diversity of its conceptual origin indicates that the fiber bundle is a central mathematical construct.
It came as a great shock to both physicists and mathematicians in the 1970s that the mathematics of gauge theory, both abelian and non-abelian, turned out to be exactly the same as that of fiber-bundle theory. 8 But it was a welcome shock because it served to bring back the close relationship between the two disciplines, a relationship that had been interrupted by the increasingly abstract nature of mathematics since the middleof the 20th century.
In 1975, after learning the rudiments of fiber-bundle theory from my mathematiciancolleague James Simons, I showed him the 1931 paper by Dirac on the magnetic monopole. He exclaimed, “Dirac had discovered trivial and nontrivial bundles before mathematicians.”
It is perhaps not inappropriate to conclude this brief sketch of the conceptual origin of gauge theory by quoting a few paragraphs from Maxwell’s tribute upon Faraday’sdeath in 1867:
The way in which Faraday made use of his idea of lines of force in co-ordinating the phenomena of magneto-electric induction shows him to have been in reality a mathematician of a very high order—one from whom the mathematicians of the future may derive valuable and fertile methods… .
From the straight line of Euclid to the lines of force of Faraday this has been the character of the ideas by which science has been advanced, and by the free use of dynamical as well as geometrical ideas we may hope for further advance… .
We are probably ignorant even of the name of the science which will be developed out of the materials we are now collecting, when the great philosopher next after Faraday makes his appearance.
REFERENCES
1. F. A. J.L. James, ed., The Correspondence of Michael Faraday, Vol. 1, Institution of Electrical Engineers (1991), p. 287.
2. J. Larmor, Proc. Cambridge Philos. Soc. 32, 695 (1937), p. 697. http://dx.do
3. T.Kinoshita, in Proceedings of the Conference in Honour of the 90th Birthday of Freeman Dyson, K. K. Phua et al., eds., World Scientific (2014), p. 148.
4. For this and the ensuing history, see C. N. Yang, in Hermann Weyl, 1885–1985: CentenaryLectures, K. Chandrasekharan, ed., Springer (1986), p. 7;and
A. C. T.Wu, C. N. Yang, Int. J. Mod. Phys. A 21, 3235 (2006). http://dx.do
5. C. N.Yang, R. Mills, Phys. Rev. 95, 631 (1954).
6. An English translation of Fermi’s original paper is available in F. L. Wilson, Am. J. Phys. 36, 1150(1968). http://dx.do
7. P. A.Schilpp, ed., Albert Einste in: Philosopher-Scientist, Open Court (1949). The two passages are English translations of Einstein’s autobiographical notes written in 1946 when Einstein was 67 years old.
8. T. T. Wu, C. N. Yang, Phys.Rev. D 12, 3845(1975). http://dx.do
C. N. Yang is the honorary director of the Institute for Advanced Study at Tsinghua University in Beijing and a Distinguished Professor-at-Large in the physics department at the Chinese University of Hong Kong.
杨振宁先生的报告发表 在2014年11月的《今日物理(Physics Today)》上,国内施郁 博士也有博文介绍。